Determine the inverse of the following matrix, if it exists.

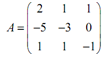
We first form the new matrix through tacking onto the 3 x 3 identity matrix to this matrix.  It is,

We will here use row operations to attempt and convert the first three columns to the 3 x 3 identity. Conversely, we need a 1 on the diagonal that begins at the upper left corner and zeroes in all the other entries into the first three columns.

If you think regarding to it, this process is very same to the process we used in the final section to resolve systems, this just goes a little farther. Now there is the work for this problem.

Therefore, we were capable to convert the first three columns in the 3 x 3 identity matrix thus the inverse exists and this is,

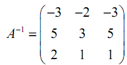
Fact

Provided a square matrix A

1.   A^-1 will exist, if A is nonsingular.

2    A^-1 will NOT exist, if A is singular.

I'll leave this to you to verify that fact for the previous two illustrations.