Example of Implicit differentiation
So, now it's time to do our first problem where implicit differentiation is required, unlike the first example where we could actually avoid implicit differentiation by solving for y.
Example Determine y′ for the following function.
x2 + y 2 = 9
Solution
Now, it is just a circle and we can solve out for y which would give,
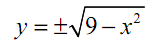
Prior to starting this problem we stated that we must do implicit differentiation here since we couldn't just solve out for y and still that's what we just did. Thus, why can't we utilize "normal" differentiation here? The problem is the " ±". With this in the "solution" for y we illustrates that y is actually two different functions. Which should we use? Should we utilize both? We just want a single function for the derivative and at best we contain two functions here.
Thus, in this example really we are going to have to do implicit differentiation thus we can ignore this. In this instance we'll do the similar thing we did in the first example & remind ourselves that y is actually a function of x and write y as y (x) . Once we've done it all we have to do is differentiate each term w.r.t x.
dx2 [y ( x )]2 / dx = d (9)/dx
As with the first example the right side is simple. The left side is also pretty simple as all we have to do is take the derivative of each of term and note as well that the second term will be same the part (a) of the second example. All we have to do for the second term is utilizes the chain rule.
After taking the derivative we contain,
2 x + 2 [y ( x ) ]1y′ ( x ) = 0
At this instance we can drop the ( x ) part since it was only in the problem to help with the differentiation procedure. The last step is to just solve the resulting equation for y′ .
2x + 2 yy′ = 0
y′ = - x /y
We can't just plug in for y as we wouldn't know which of the two functions to utilization. Most answers from implicit differentiation will include both x & y so don't get excited regarding that when it happens.