Example: Joanne is given a four-question multiple-choice quiz.  She hasnt studied the material to be quizzed, so she decides to answer the questions by randomly guessing the answers without reading the questions or the answers. 

1. What is the probability that Joanne answered all of the questions correctly?
2. What is the probability that Joanne chose wrong answers for all of the questions?

Solution:

Let X be the number of correct answers on the quiz.  Then X can be 0, 1, 2, 3, or 4.  Since each question has five possible answers and only one correct answer, the probability of choosing the correct answer for a question is 1/5.  The probability of choosing the incorrect answer is 4/5.

P(X = 4) is the probability that all of the questions were answered correctly. The events are independent because each question is separate event.

P(X = 0) is the probability that all of the questions were answered incorrectly.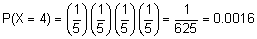

This tree diagram shows all of the possible outcomes for this experiment as well as the difference values of the random variable.

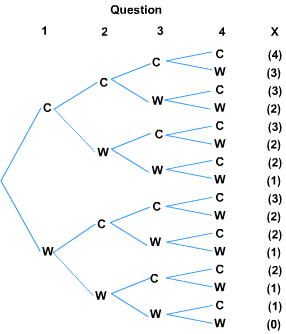
From this diagram, you can see that there are four occurrences of one correct answer (X = 1).  We can list all of the remaining probabilities with the help of the tree diagram.

In general: 
P(X = x) is the product of three factors:

1. The number of ways that exactly X successes can occur in a set of n trials.
2. The probability of having X successes.
3. The probability that failure will occur the remaining (n'X) trials.