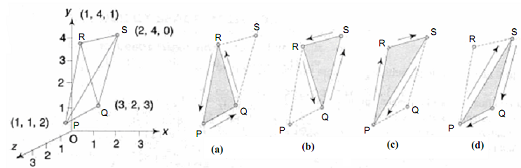
Example of Back Face Detection Method

To illustrate the method, we shall start with the tetrahedron (pyramid) PQRS of     Figure with vertices P (1, 1, 2), Q (3, 2, 3), R (1, 4, 1), and S (2, 4,0). It is obviously a convex object, re-entrant angles just not being possible with triangles. In this case we may be able to guess that the vertex S is behind the triangle PQR, and also that faces PQR and QRS are visible, and the other two faces PQS and PRS are hidden. But the computer must be able to decide for itself and we too cannot decide for more than one tetrahedron. So, let us start with the order PQR as counter-clockwise with the triangle facing the viewer, as shown by the arrows along the edges in Figure. Then, for the adjacent triangle QRS, at its common edge QR with the triangle PQR, the arrow must point in the opposite direction, namely from R to S as shown, and hence the vertices must indeed be ordered as RQS (or QSR, or SRQ), as in Figure 3.3(b).

The vertex sequences of the other two triangles are also followed by the same logic : For the  trianglePRS, from the common edge PR with triangle PQR, the vertex sequence must be PRS (or RSP, or SPR), as in Figure. We could have also used the common edge RS with triangle QRS to get the same result. For triangle PQS, from anyone of the three common edges with the other three triangular faces, the vertex sequence will be determined as PSQ (or SQP, or QPS), as in Figure.