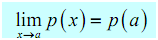Calculate the value of the following limit.

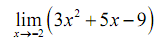
Solution: This first time through we will employ only the properties above to calculate the limit. Firstly we will employ property 2 to break up the limit in three separate limits. Then we will employ property 1 to bring the constants out of the first two limits.  Doing this gives us,

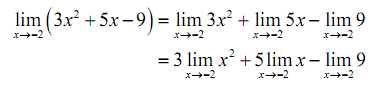
Now we can use properties 7 through 9 to in fact compute the limit.

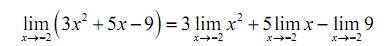
                                            = 3( -2)² + 5 ( -2) - 9

                                             =  -7

Now, let's note down that if we had defined

p ( x ) = 3x² + 5x - 9

then the proceeding instance would have been,

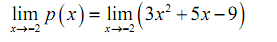
= 3 (-2)²  + 5 ( -2) - 9

= -7

= p ( -2)

In other terms, in this case we illustrates that the limit is the similar value that we'd get just by evaluating the function at the point in question. It seems to violate one of the main concepts regarding limits that we've seen to this point.

In the earlier two sections we made a great deal regarding the fact that limits do not care about what is happening at the point in question. They simply care about what is happening around the point. Therefore how does the earlier example fit into this since it appears to violate this main idea regarding limits?

All polynomials are "nice enough" so that what is happening around the point is accurately the similar as what is happening at the point. It leads to the following fact.

Fact

If p(x) is polynomial then,