Evaluate the principal stresses and principal planes:

The state of stress at a point in a loaded solid is prescribed on two faces of an element whose shape is a triangular prism as display in Figure. Evaluate the principal stresses and principal planes.

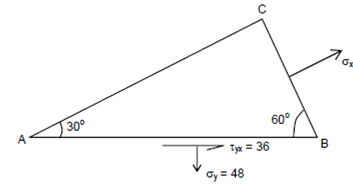
Figure

Solution

Here, we have to first obtain the value of x and subsequent calculations will be a standard set.

Given   σ_y = 48 MPa

τ_yx = 36 MPa            ∴  τ_xy = - 36 MPa

σ30^o = 60 MPa (aspect angle of plane BC is + 30^o)

σ30° = (σ_x +σ_y/2) +(σ_x -σ_y/2) cos (2× 30°) +τ_xy sin (2 × 30°)

60 = (σ_x + 48/2) + (σ_x  - 48/2) cos 60^o  + (- 36) sin 60^o

60 = σ_x/2 + 24 +σ_x/2 cos 60° -24 cos 60° -36 sin 60°

i.e. 60 = σ_x/2 (1+ cos 60°) +24 -24 cos 60° -36 sin 60°

∴          σ_x =2/1+0.5 [60-24-(-24×0.5)-(-36)× 0.866]

= 2/1.5[79.177] = 105.57 MPa

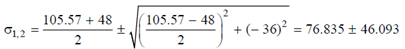
∴ σ₁ = 76.835 + 46.093 =122.928 MPa

σ₂ = 76.835 - 46.093 =30.742 MPa

Let the aspect angles of the principal planes be Φ

tan 2Φ = 2τ_xy/σ_x  - σ_y = 2 × (- 36)/105.57 - 48 = -51.35° or 128.65°

Φ = - 25.675° or 64.325°

Substituting Φ = - 25.675^o (or 2Φ = - 51.35^o) in expression for σn

σn = (105.57 + 48/2 ) + (105.57 - 48/2) cos (- 51.35^o ) - 36 sin (- 51.35^o )

= 122.92 MPa

∴ Φ₁ = - 25.675^o and Φ₂ = 64.325^o