Evaluate the point of contraflexure:

An overhanging beam of 15 m span is carrying a consistently distributed load of 1 kN/m over the length of 10 m at a distance 5 m from the left free end and point loads 7 kN and 4 kN, at free end and at a distance 2 m from the free end, respectively. Sketch the BMD and SFD for the beam. Situate the point of contraflexure.

Solution

Taking moments around B and equating to zero,

R _A   × 10 - (7 × 15) - (4 × 13) - (1 × 10 × (10/2) ) = 0

R_A = 20.7 kN

and      R_B = 7 + 4 + (1 × 10) - 20.7 = 0.3 kN

Shear Force (beginning from the left end C)

SF just right of C, F_C = - 7 kN

SF just left of D, F_D = - 7 kN

SF just right of D, F_D = - 7 - 4 = - 11 kN

SF just left of A, F_A = - 11 kN

SF just right of A, F_A = - 11 + 20.7 = 9.7 kN

SF just left of B, F_B = + 9.7 - (1 ×10) = - 0.3 kN = Reaction at the support B.

Bending Moment      

BM at B, MB = 0

 BM at A, M_A

= (0.3 × 10) - (1 × 10 × (10/2))  = - 47 kN m

BM at D, M_D = - (7 × 2) = - 14 kN m

BM at C, M_C  = 0

let a section XX at a distance x from the end B as illustrated in Figure.

Shear force at section XX,

F_x = - 0.3 + 1(x)

For maximum bending moment, shear force will be zero.

- 0.3 + x = 0

x = 0.3 m

We have,

M_x = + 0.3(x) - 1 × (x) ×(x/2) = 0.3x - x ² /2

M_max = 0.3 × (0.3) - ((0.3)² /2) = + 0.045 kN m

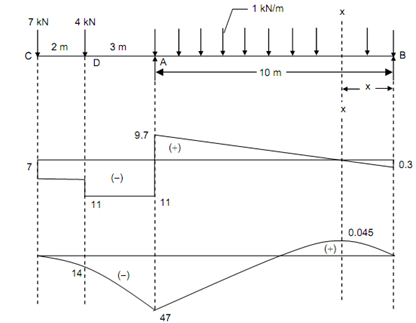
Figure

This is seen that the maximum negative bending moment take place at A and maximum positive bending moment take place at a distance 0.3 m from the right end B.

M_max (positive) = + 0.045 kN m

M_max (negative) = - 47 kN m

Point of Contraflexure

This is observed that the BM changes sign among A and B,

BM at any section XX,

M_x = 0.3 x - x ² / 2

Equating this to zero,

0.3 x - x²/2      = 0

0.6 x - x²    = 0

∴          x = 0.6 m

Thus, the point of contraflexure is at a distance of 0.6 m from the right end B.