Evaluate the motion of the system:

If in above Example, the block A is resting on an inclined plane at 45^o to horizontal as illustrative in Figure, find out the motion of the system assuming μ = 0.1.

Solution

Supposing that block A moves upwards a distance s while B moves downwards by (s/2) as before as shown in Figure

N _A  = W_A  cos 45^o

= 400 × 0.707

= 283 N.

Friction = 0.1 × 283

By using the principle of conservation of energy & letting datum level as B′ which is the final position of B,

W_A   (H + (s/2))+ W_B× (s/2) = W_A ( H + (s /2)+ s × sin α + (1/2)M _A  V ²  +(1/2)M_B (V/2)² + 28 × s

∴ 10 × g ( s/2)   - 40 × 0.707 s - 28 × s = V ²  (40 +(10/4))

By using equation of motion of uniform acceleration a,

                  V ² = 2 a s   (since initial velocity is zero)

∴ approximately   49 - 28 - 28 = a (42.5)

 ∴ a = - 7 /42.5 m / sec²

Negative sign indicates that assumed direction of motion of A is not right and therefore the block A moves downward. As direction of friction also changes (that means upwards), the magnitude of acceleration is recomputed separately.

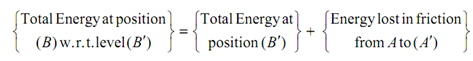
The system while A moves down through distance s, its  velocity is V while Block B moves up with velocity (V/2) considering initial- position of Block B as datum level,

                                        V ² = 2 (a × s)

Where,            a = acceleration of A,

W_A (H) = W [H - s (sin α)] + W_B (s/2) + 40(V²/2)         + (10/2) (V²/4) + F × s

∴ 0 = - 40 × (s × 0.707) × 9.8 + 10 × (9.8 × s)/2 + (V² /2) (42.5) + 28 s

∴ 0 = s [(- 280 + 49 + 28) + a × 42.5]

Taking 277.14 ≈ 280

 ∴ a = 203 /42.5

≈ 4.7 m / sec².

Hence, Block A moves down with acceleration of 4.7 m/sec².