Evaluate the maximum bending stresses:

A beam of I-section illustrated in Figure is simply supported over a span of 10 m. It carries an uniform load of 4 kN/m over the whole span. Evaluate the maximum bending stresses.

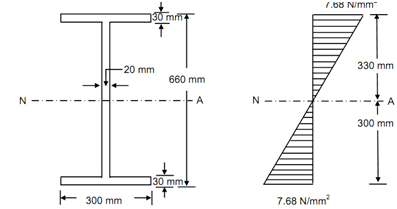
   Cross-section of Beam                 Bending Stress Distribution

Figure

Solution

Moment of inertia, I =1/12  (BD³ - bd³)

=          (1/12) (300 × 660³ - 280 × 600³)

= 21.474 × 10⁸ mm⁴

Span of beam, l = 10 m

Uniformly distributed load, w = 4 kN/m

Maximum bending moment at the centre of beam, M = wl ²/ 8

Therefore,        M =4 × 10 ² / 8

= 50 kN m

= 5 × 10⁷ N mm

Neutral axis passes by the centroid of I-section.

 The distance of top and bottom layer from neutral axis, y = 330 mm

Thus, Bending stress, σ = (M / I )× y

= (5 × 10 ⁷ / 21.474 × 10⁸ )× 330 = 7.68 N/mm²

So the bending stress at top and bottom layers = 7.68 N/mm².