Example:  If c ≠ 0 , evaluate the subsequent integral.

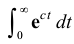
Solution

Remember that you require converting improper integrals to limits as given,

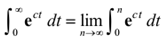
Here, do the integral, so evaluate the limit.

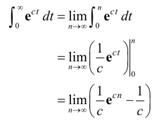
Here, at this point, we've found to be careful. The value of c will influence our answer. We've previously assumed that c was non-zero, this time we need to worry regarding to the sign of c. If c is positive the exponential will be present at infinity. Conversely, if c is negative the exponential will go to zero.

Therefore, the integral is only convergent that is the limit exists and is finite provided c<0.  Under this case we find,

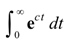
= -(1/c), given c< 0 .........(2)

Here we remember about how to do these, let's calculate some Laplace transforms. We'll start off along with probably the simplest Laplace transform to calculate.