Use the mirror equation to deduce that:
(a) an object placed between f and 2 f of a concave mirror produces are al image beyond 2f.
(b) a convex mirror always produces a virtual image independent of the location of the object.
(C)the virtual image produced by a convex mirror is always diminished in size and is located between the focus and the pole.
(d) An object placed between the pole and focus of a concave mirror produces a virtual and enlarged image.
[Note: This exercise helps you deduce algebraically properties of images that one obtains from explicit ray diagrams.]
Answer
(a) For the concave mirror the focal length (f) is negative.
f < 0.
When an object is placed on the left side of the mirror the object distance (u)is negative. U < 0
For image distance v, we are able to write the lens formula as:
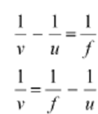
The object lies between f and 2 f.
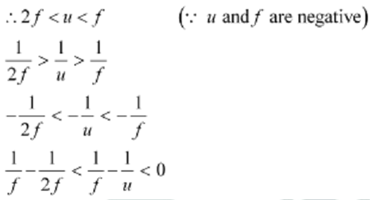
Using equation (1),we get:
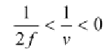
1 / v Is negative, i.e., v is negative.
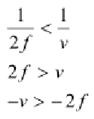
Therefore, the image lies beyond 2 f.
(b) For a convex mirror, the focal length (f)is positive. f>0
When an object is placed on the left side of the mirror the object distance (u)is negative. u<0
For image distance v ,we have the mirror formula:
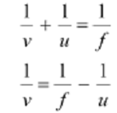
But we have u <0
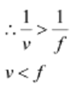
Hence the image formed is diminished and is located between the focus (f) and the pole.
(d)For a concave mirror, the focal length (f) is negative. f<0
When an object is placed on the left side of the mirror the object distance (u)is negative. u<0
It is placed between the focus ( f)and the pole.
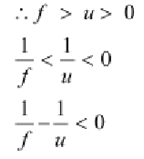
For image distance v, we have the mirror formula:
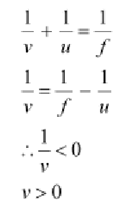
The image is formed on the right side of the mirror. Therefore it is a virtual image.
For u< 0 and v > 0 we are able to write:
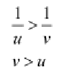
Magnification m = v/u > 1
Therefore the formed image is enlarged.