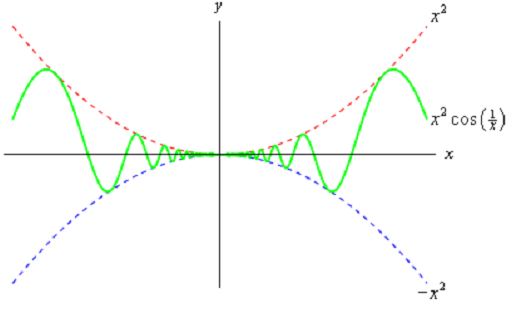
Evaluate the given limit.

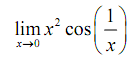
Solution: In this question none of the earlier examples can help us. There's no factoring or simplifying to accomplish.  We can't rationalize & one-sided limits won't work. There's still a question as to whether this limit will present as we have division by zero within the cosine at x=0.

The firstly thing to notice is that we know the given fact about cosine.

                                                -1 ≤ cos ( x )≤ 1

Our function doesn't contain just an x in the cosine, however as long as we ignore x =0 we can say the similar thing for our cosine.

                                                       -1 ≤ cos ( 1/x ) ≤ 1

It's okay for us to avoid x = 0 here since we are taking a limit and we know which limits don't care regarding what's in fact going on at the point in question, x = 0 in this case.

Now if we have the above inequality for our cosine we can only multiply everything by an x² and get the following.

                                             - x²  ≤ x² cos ( 1/x ) ≤ x²

In other terms we've managed to squeeze the function which we were interested in among two other functions which are very easy to deal with.  Hence, the limits of the two outer functions are.

These are the similar and hence by the Squeeze theorem we has to also have,

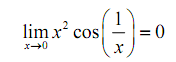
We can check this with the graph of the three functions.  This is illustrated below.