The position of an object at any time t (in hours) is specified by,

s (t ) = 2t ³ - 21t ² + 60t -10

Find out when the object is moving to the right and whiles the object is moving to the left.

 Solution : The single way that we'll know for sure which direction the object is moving is to contain the velocity in hand.  Recall that if the velocity is +ve the object is moving off towards the right and if the velocity is negative then the object is moving toward the left.

Thus, we need the derivative as the derivative is the velocity of the object. The derivative is following,

s′ (t ) = 6t ² - 42t + 60 = 6 (t ² - 7t + 10)= 6 (t - 2) (t - 5)

The cause for factoring the derivative will be clear shortly.

Now, we have to determine where the derivative is positive & where the derivative is negative. There are many ways to do this.

Since polynomials are continuous we  already know from the  Intermediate Value Theorem that if the polynomial ever changes sign then it should have first gone through zero.  hence, if we knew where the derivative was zero we would know the just points where the derivative should change sign.

We can illustrates from the factored form of the derivative which the derivative will be zero at t = 2 and t = 5 .  Let's plot these points on a number line.

Now, we can illustrate that these two points divide the number line in three distinct regions.  In each region we know that the derivative will be the similar sign.  Recall the derivative can only change sign at the two points which are utilized to divide the number line up into the regions.

So, all that we have to do is to check the derivative at a test point in each of region and the derivative in that region will have the similar sign as the test point. Following is the number line along with the test points and results illustrated.

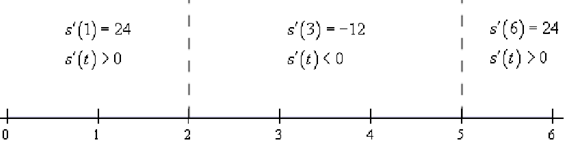
Following are the intervals wherein the derivative is positive and negative.

positive : -∞ < t < 2  &  5 < t < ∞

negative :         2 < t < 5

We involved negative t's here since we could even though they may not make much sense for this problem.  Once we know it we also can answer the question. The object is moving to the right & left in the given intervals.

moving to the right : -∞ < t < 2  &  5 < t < ∞

moving to the left  :    2 < t < 5