Equilibrium in a single market model

A single market model has three variables: the quantity demanded of the commodity (Q_d), the quantity supplied of the commodity (Q_s) and the price of the commodity (P).  equilibrium is assumed to hold in the market when the quantity demanded (Q_d) = Quantity Supplied (Q_s) .  It is assumed that both Q_d and Q_s are functions.  A function such as y = f (x) expresses a relationship between two variables x and y such that for each value of x there exists one and only one value of y.  Q_d is assumed to be a decreasing linear function of P which implies that as P increases, Q_d decreases and Vice Versa.  Q_s on the other hand is assumed to be an increasing linear function of P which implies that as P increases, so does Q_s.

Mathematically, this can be expressed as follows:

Q_d = Qs

Q_d = a - bP where a,b > 0. ............................(i)

Q_s = -c + dp where c,d >0. ...........................(ii)

Both the Q_d and Q_s functions in this case are linear and can be expressed graphically as follows:

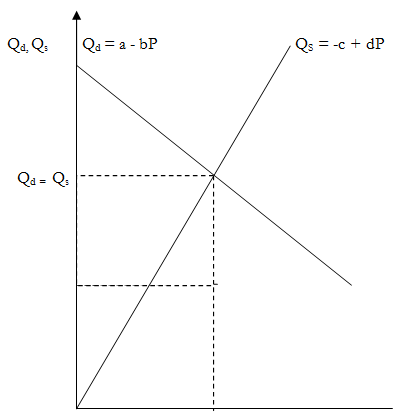
Once the model has been constructed it can be solved.

At equilibrium,

Qd = Qs

\a - bP = -c + dP

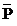 = a + c

        b + d

To find the equilibrium quantity 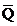, we can substitute into either function (i) or (ii).

Substituting 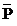 into equation (i) we obtain:

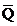 = a - b (a+c) = a (b+d) - b (a+c) = ad -bc

              b + d                 b + d             b + d

Taking a numerical example, assume the following demand and supply functions:

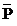 = 100 - 2P

Q_s = 40 + 4P

At equilibrium, Q_d = Q_s

100 - 2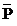 = 40 + 4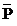

              6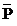 = 60

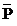             = 10

Substituting P = 10, in either equation.

Q_d = 100 - 2 (10) = 100 - 20 = 80 = Q_s

A single market model may contain a quadratic function instead of a linear function.  A quadratic function is one which involves the square of a variable as the highest power.  The key difference between a quadratic function and a linear one is that the quadratic function will yield two solution values.

In general, a quadratic equation takes the following form:

ax² + bx + c = 0 where a ¹ 0.

Its two roots can be obtained from the following quadratic formula:

X₁, X₂ = -b + √( b² - 4ac)

                        2a

Given the following market model:

Q_d = 3 - P²

² = 6P - 4

At equilibrium:

3 - P² = 6P - 4

P² + 6P - 7 = 0

Substituting in the quadratic formula:

a =1, b = 6, c = -7

= - 6 +Ö 6² - 4 (1 x - 7)

                2 x 1

= 

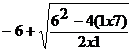
P = 1 or -7 (ignoring -7 since price cannot be negative)

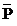 = 1

Substituting 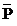 = 1 into either equation:

Q_d = 3 - (1)² = 2 = Q_s

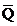 = 2