Equations of Planes

Earlier we saw a couple of equations of planes.  Though, none of those equations had three variables in them and were actually extensions of graphs which we could look at in two dimensions. We would like a much more general equation for planes.

Thus, let us start by assuming that we know a point that is on the plane, P₀ = (x₀, y₀, z₀).  Let's as well suppose that we have a vector that is orthogonal (perpendicular) to the plane, n = (a, b, c). This vector is known as the normal vector.  Now, suppose that P = (x, y, z) is any point in the plane. At last, as we are going to be working with vectors initially we'll let ^→r₀ and ^→r be the position vectors for P₀ and P correspondingly.

Here is a diagram of all these vectors.

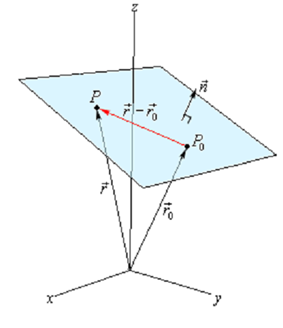
Note that we added in the vector ^→r - ^→r₀ that will lie completely in the plane.  As well notice that we put the normal vector on the plane, but in fact there is no reason to expect this to be the case. We put it here to demonstrate the point.  It is totally possible that the normal vector does not touch the plane in any way.

Here now, as n is orthogonal to the plane, it's as well orthogonal to any vector that lies in the plane.  Particularly it's orthogonal to ^→r -^→r₀.  Remind from the Dot Product section which two orthogonal vectors will comprise a dot product of zero.  Alternatively,

n^→.(^→r -^→r₀) = 0          =>^→n. ^→r =^→n. ^→r₀

This is known as the vector equation of the plane.