Energy Bands
1) Since isolated atoms are brought together to make a solid, the electron wave functions begin to overlap.
2) Several interactions occur, and, at the proper interatomic spacing for the crystal, the forces of attraction and repulsion find a balance.
3) Because of Pauli Exclusion Principle, the discrete energy levels of individual atoms split into bands relating to the pair instead of to individual atoms.
4) In a solid, because of large number of atoms, the split energy levels for necessarily continuous bands of energy.
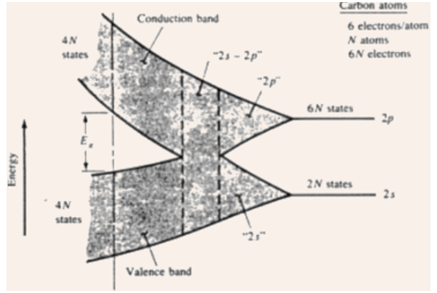
Figure: Splitting of individual energy levels to energy bands as atoms are brought closer together.
5) Imaginary creation of a diamond crystal from isolated carbon atoms (1s22s22p2).
6) Every atom has two 1s states, two 2s states, six 2p states, and higher states.
7) For N atoms, the no. of states are 2N, 2N, and 6N of type 1s, 2s, and 2p respectively.
8) Along with a reduction in the interatomic spacing, these types of energy levels split into bands, and the 2s and 2p bands merge into a single band comprising 8N available states.
9) Since the interatomic spacing arrives at the equilibrium spacing of diamond crystal, this band splits into two bands separated by an energy gap Eg, in which no allowed energy states for electrons exists => forbidden gap.
10) The upper band (termed as the conduction band) and the lower band (termed as the valence band) contain 4N states each.
11) The lower 1s band is filled along with 2N electrons, though the 4N electrons residing in the original n = 2 states will now inhabit states either in the valence band or in the conduction band.
12) At 0 K, the electrons will inhabit the lowest energy states available to them => so, the 4N states in the valence band will be totally filled, and the 4N states in the conduction band will be totally empty.