Q. Effect of feedback on dynamic response and bandwidth?

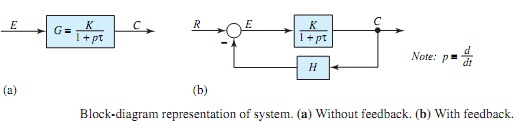
Let us consider the block-diagram representation of the open-loop system shown in Figure 16.2.5(a), whose direct transfer function is given by

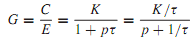
corresponding to which, the transient solution of the system is of the form given by

c(t) = Ae^-t/τ

The transient in this system is seen to decay in accordance with a time constant of τ seconds. By placing a feedback path H around the direct transfer function, as shown in Figure (b), the closed-loop transfer function is then

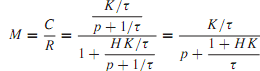
and the corresponding transient solution of the closed-loop system is of the form

c_f (t) = A_fe^{-[(1+HK)/τ ]t}

where c_f(t) represents the transient response of the output variable with feedback. Comparing Equations, it is clear that the time constant with feedback is smaller by the factor 1/(1 + HK), and hence the transient decays faster.

By treating the differential operator p as the sinusoidal frequency variable jω, i.e., p = jω = j(1/τ ), it follows from Equation that the bandwidth of the open-loop system spreads over a range fromzero to a frequency of 1/τ rad/s. On the other hand, for the system with feedback, Equation reveals that the bandwidth spreads from zero to (1 + HK)/τ rad/s, showing that the bandwidth has been augmented by increasing the upper frequency limit by 1 + KH.