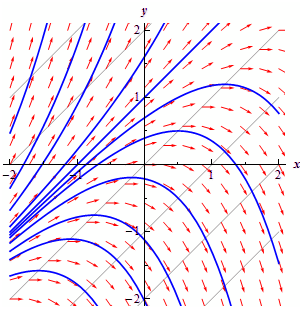
Draw the direction field for the subsequent differential equation. Draw the set of integral curves for this differential equation.

 Solution:

 y′ = y - x

 To draw direction fields for this type of differential equation we initially know places where the derivative will be constant. To complete this we set the derivative into the differential equation equivalent to a constant, as c. It provides us a family of equations, termed as isoclines, which we can plot and on each of these curves the derivative will be a constant value of c.

Remember here that in the previous illustrations we looked at the isoclines for c = 0 to find the direction field started. In our case the family of isoclines is as:

c = y - x

These curve's graph for several values of c is demonstrated below.

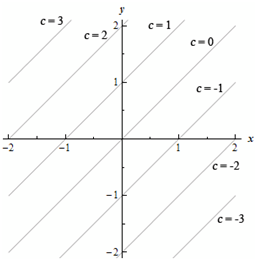
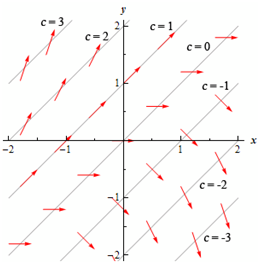
Here, on each of these lines, or isoclines, the derivative will be not change and will have a value of c. At c = 0 isoclines the derivative will all the time have a value of zero and thus the tangents will all be horizontal. At c = 1 isoclines the tangents will all the time have a slope of 1 and at c = -2 isoclines the tangents will all the time have a slope of -2 and so on. Below is some tangents place in for each of these isoclines.

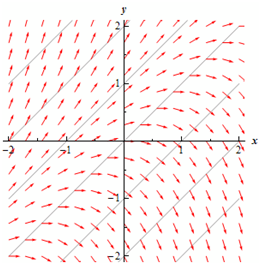
To add extra arrows for those areas among the isoclines start at say, c = 0 and move up to c = 1 and when we do this we raise the slope of the arrows or tangents from 0 to 1. It is demonstrated in the figure below.

We can after that adds in integral curves as we did in the previous illustrations. It is demonstrated in the figure below.