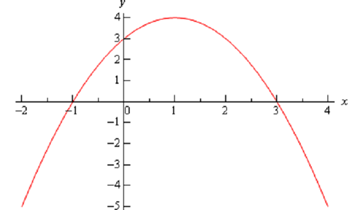
Graph        f ( x ) = - x² + 2x + 3 .

Solution

It is a parabola in the general form.

                             f ( x ) = ax² + bx + c

In this form, the x-coordinate of the vertex (on the parabola the highest or lowest point) is

x = -  b/2a and we get the y-coordinate is y = f ( -  b/2a)  .  Hence, for our parabola the coordinates of the vertex will be.

x= - 2/(2(-1)=1

y=f(1) = -(1) 2 + 2(1) +3=4

Hence, the vertex for this parabola is (1,4).

We can also find out which direction the parabola opens from the sign of a.  If a is +ve the parabola opens up & if a is -ve the parabola opens down.  In our case the parabola opens down.

Now, since the vertex is above the x-axis & the parabola opens down we know that we'll have x-intercepts (that means values of x for which we'll have f ( x ) = 0 ) on this graph.  Hence, we'll solve  out the following.

- x² + 2 x + 3 = 0

x² - 2 x - 3 = 0

( x - 3) ( x + 1) = 0

Hence, we will have x-intercepts at x = -1 and x = 3 . Notice as well that to make our life simple in the solution process we multiplied everything by -1 to get the coefficient of the x²  positive.  It made the factoring easier.

Following is a sketch of this parabola.