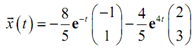DISTINCT EIGENVALUES -SYSTEM SOLVING:

Example

Solve the following IVP.

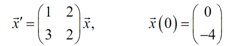
Solution:

Therefore, the first thing that we must to do that is, get the eigenvalues for the matrix.

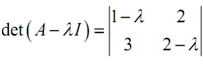
= l² -3l - 4

= (l+ 1) (l- 4)                                     ⇒                     l₁ = -1,  l₂ = 4

Here let's get the eigenvectors for each of these.

For l₁ = -1,

We have to solve:

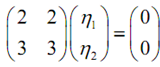
= 2h₁ + 2h₂                              ⇒                                 h₁ = - h₂

The eigenvector for this case is,

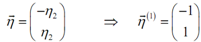
= h₂= 1,

For l₂ = 4,

We have to solve:

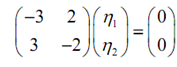
⇒ = -3h₁ + 2h₂ = 0                              ⇒                                 h₁ =( 2/3) h₂

The eigenvector for this case is,

= h₂ = 3

So the general solution is after that,

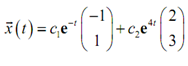
Now, we have to get the constants. To do that we simply have to apply the initial conditions

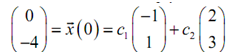
All we required to do now is multiply the constants with and we after that get two equations that is one for each row which we can solve for the constants. It gives,

-c₁ + 2c₂ = 0;

c₁ + 3c₂ = -4;

By solving both equations we get:

c₁ = -(8/5) and c₂ = (-4/5)

The solution is subsequently,