Sketch the phase portrait for the given system.

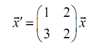
Solution:

From the last illustration we know that the eigenvectors and eigenvalues for this system are,

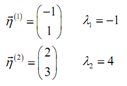
This turns out; it is all the information which we will require to sketch the direction field.  However we will relate things back to our solution hence we can notice that things are going correctly.

We'll start through sketching lines which follow the direction of the two eigenvectors. It gives,

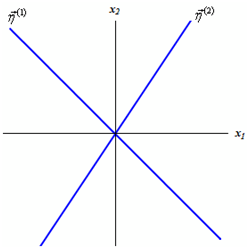
Here, from the first illustration our general solution is,

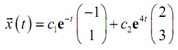
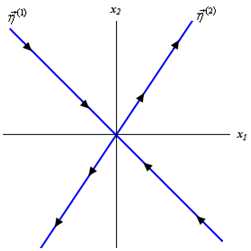
If we have c₂ = 0 so that the solution is an exponential times a vector and all that the exponential does is affect or influence the magnitude of the vector and the constant c1 will have an effect on both the sign and the magnitude of the vector. Conversely, the trajectory under this case will be a straight line which is, parallel to the vector, ?h⁽¹⁾_. Also see that as t rises the exponential will get smaller and much smaller and thus the trajectory will be moving in directions of the origin. If c₁>0 the trajectory will be present in Quadrant II and if c₁<0 the trajectory will be present in Quadrant IV.

Therefore the line in the graph above marked by ?h⁽¹⁾ will be a sketch of the trajectory consequent to c2 = 0 and this trajectory will approach the origin as t raises.

If we this time turn things around and see the solution corresponding to containing c₁ = 0 we will have a trajectory which is parallel to ?h⁽²⁾.  Also, since the exponential will rise as t raises and so in this case the trajectory will now move away from the origin as t rises. We will denote it with arrows on the lines into the graph above.

Remember that we could have found this information with truly going to the solution. All we actually require to do is look at the eigenvalues. Eigenvalues this are negative will correspond to solutions which will move in directions of the origin as t rises in a direction which is parallel to its eigenvector. Similarly eigenvalues this are positive move away from the origin as t rises in a direction which will be parallel to its eigenvector.

If both constants are into the solution we will contain a combination of these behaviors. For huge negative t's the solution will be dominated through the portion which has the negative eigenvalue as in these cases the exponent will be huge and positive. Trajectories for huge negative t's will be parallel to ?h⁽¹⁾ and moving in similar direction.

 Solutions for large positive t's will be dominated through the portion with the positive eigenvalue. Trajectories under this case will be parallel to ?h⁽²⁾ and moving in similar direction.

Generally, it looks like trajectories will start "near" ?h⁽¹⁾, move in towards the origin and after that as they get closer to the origin they will start moving in directions of ?h⁽²⁾ and then continue up along that vector.  Sketching several of these in will provide the following phase portrait. Now there is a sketch of this along with the trajectories consequent to the eigenvectors marked in blue.

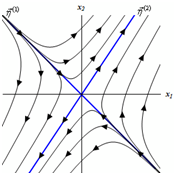
During this case the equilibrium solution (0, 0) is termed as a saddle point and is unstable. During this case unstable implies that solutions move away from this as t increases.