Determine the value of maximum bending moment:

Draw the shear force & bending moment diagrams for the beam overhanging on both of sides as illustrated in Figure. Determine the magnitude of maximum positive and maximum negative bending moment and also situate the point of contraflexure, if any exist.

Solution

Letting right side, take moments around A,

M_A = R_B × 12 - 2 × 12 × 10

M_A = 12 R_B - 240

Considering left side, take moments about A,

M_A = - 6 × 4 = - 24 kN m

Equating these two values, we get the reaction at the support B,

12 R_B - 240 = - 24

R_B = 18 kN

R_A = 6 + (2 × 12) - R_B = 30 - 18 = 12 kN

Shear Force (Starting from the left end C)

SF at C, F_C = - 6 kN

SF just left of A, F_A = - 66 kN

SF just right of A, F_A = - 6 + 12 = + 6 kN

SF at D, F_D = + 6 kN

SF just left of B, F_B = + 6 - (2 × 8) = - 10 kN

SF just right of B, F_B = - 10 + 18 = + 8 kN

SF at E, F_E = + 8 - (2 × 4) = 0.

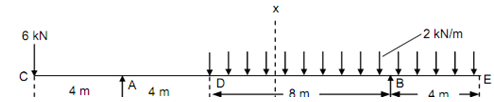
Figure

BM at C and E, M_C  = M_E = 0

BM at B, M_B = - ( 2 × 4 × (4/2) )  = - 16 kN m

BM at D, M_D =+ (18 × 8) - ( 2 × 12 × (12/2)  = 0

BM at A, M_A = - (6 × 4)  = - 24 kN m

Maximum Bending Moment

Let a section XX at a distance 'x' from the end E. SF at section XX,

F_x = - 18 + 2x

For maximum bending moment, F_x must be zero.

- 18 + 2x = 0

∴          x = 9 m

BM at any section XX among D and B,

M_x = 18 (x - 4) - 2x ×(x/2)

= 18 (x - 4) - x²

M_max = 18 (9 - 4) - 9²  = 9 kN m

Maximum negative bending moment = -24 kN m

Maximum positive bending moment = + 9 kN m

Points of Contraflexure

Assume M and D is the points of contraflexure where the BM changes sign.

To determine the position of M, equate the moment equation among D and B to zero.      

                        18 (x - 4) - x² = 0

                        - x² + 18x - 72 = 0

or,                     x² - 18x + 72 = 0

We obtain,       x = 6 m and x = 9 m.

There are two points of contraflexure, one of at a distance of 6 m & the other at a distance of 9 m from the end E.