Determine the tangent line to f ( x ) = 15 - 2x2 at x = 1.
Solution : We know from algebra that to determine the equation of a line we require either two points onto the line or a single point on the line & the slope of the line. As we know that we are after a tangent line we do have a point i.e. on the line. The tangent line & the graph of the function have to touch at x = 1 hence the point (1, f (1)) = (1,13) have to be on the line.
Now we reach the problem. It is all that we know regarding the tangent line. To find the tangent line we require either a second point or the slope of the tangent line. As the only cause for needing a second point is to let us to find the slope of the tangent line let's just concentrate on seeing if we can find out the slope of the tangent line.
At this point in time all that we're going to be capable to do is to obtain an estimate for the slope of the tangent line, however if we do it properly we must be able to get an estimate that is actually the actual slope of the tangent line. We'll do it by beginning with the point that we're after, let's call it P = (1,13) . Then we will pick another point which lies on the graph of the function, let's call that point Q = ( x, f ( x )) .
For the sake of argument let's choose x = 2 and so the second point will be Q = ( 2, 7 ) .
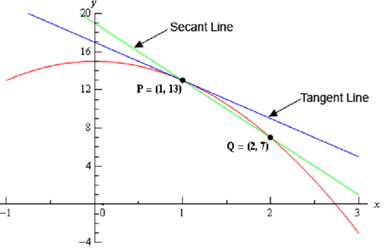
Following is a graph of the function, the tangent line & the secant line which connects P and Q.
We can illustrate from this graph that the secant & tangent lines are somewhat alike and so the slope of the secant line have to be somewhat close to the actual slope of the tangent line. Hence, as an estimate of the slope of the tangent line we can employ the slope of the secant line, let's call it mPQ ,which is,
mPQ = f ( 2) - f (1)/2-1 =7 -13/1=-6
Now, if we weren't too interested in correctness we could say it is good sufficient and use this as an estimation of the slope of the tangent line. Though, we would like an estimate that is at least rather close the actual value. Thus, to get a better estimate we can take an x i.e. closer to x = 1 and redo the work above to obtain a new estimate on the slope. Then we could take a third value of x even closer thus far and get an even better estimate.
In other terms, as we take Q closer & closer to P the slope of the secant line connecting Q and P has to be getting closer & closer to the slope of the tangent line. If you are viewing it on the web, the image below illustrates this process.
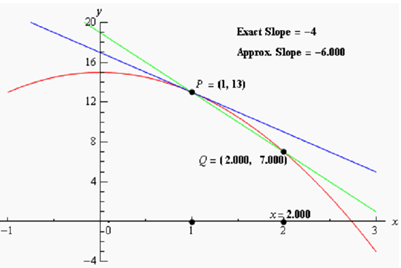
As you can illustrates (if you're reading this on the web) as we moved Q in closer & closer to P the secant lines does begin to look more & more like the tangent line and hence the approximate slopes (that means the slopes of the secant lines) are getting closer & closer to the exact slope. We'll be calculating the approximate slopes soon and we'll be capable to calculate the exact slope in a few sections.
In this figure only we looked at Q's which were to the right of P, however we could have just as easily utilized Q's that were to the left of P and we would have received the similar results. Actually, we must always take a look at Q's that are on both sides of P. In this case the similar thing is happening on both of sides of P. However, eventually we will see that doesn't have to happen. Thus we have to always take a look at what is happening on both sides of the point in question while doing this kind of procedure.
Thus, let's see if we can come up along with the approximate slopes, and therefore an estimation of the slope of the tangent line. to simplify the procedure a little let's get a formula for the slope of the line among P & Q, mPQ , which will work for any x that we have to work with. We can obtain a formula by determining the slope among P and Q using the "general" form of Q = ( x, f ( x )) .
mPQ = f ( x ) - f (1) /x -1 = 15 - 2x2 -13 /x -1 =2 - 2x2 /x -1
Now, let's pick some values of x getting closer & closer to x = 1 , plug in and get some slopes.
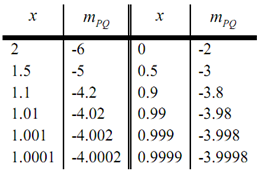
Thus, if we take x's to the right of 1 & move them in extremely close to 1 it seem that the slope of the secant lines seems to be approaching -4. Similarly, if we take x's to the left of 1 & move them in extremely close to 1 the slope of the secant lines again seem to be approaching -4.
Depending on this evidence it appear that the slopes of the secant lines are approaching -4 as we move in towards x = 1 , hence we will estimate which the slope of the tangent line is also -4. As noted above, it is the correct value & we will be capable to prove this eventually.
Now, the equation of the line which goes through (a, f ( a )) is given by
y = f ( a ) + m ( x - a )
Thus, the equation of the tangent line to f ( x ) = 15 - 2x2 at x = 1 is
y = 13 - 4 ( x -1) = -4x + 17