Determine the solution to the following differential equation.

x² y′′ + 3xy′ + 4 y = 0

 Solution

Find the roots to (3) first as generally.

r(r -1) + 3r + 4 = 0

r² + 2r + 4 = 0                          ⇒                     r_1,2 = -1 + √(3i)

Then the general solution is,

y(x) = c₁ x^-1 cos (√3 ln x ) + c₂ x^-1 sin (√3 ln x ) = x^-1 (c₁ cos (√3 ln x ) + c₂ sin (√3 ln x ))

We must now talk about how to deal along with x<0 as it is a possibility on occasion. To deal with it we require using the variable transformation,

h = - x

In this case as x<0 we will find h>0. Now, describe as,

u (h) = y(x) = y (-h)

So using the chain rule we can notice that,

u′ (h) = - y′(x)

 And u′′(h) = y′′(x)

 With this transformation the differential equation turns into,

a (-h)2 u′′ + b (-h)(-u′) + cu = 0

ah²u′′ + bhu′ +cu = 0

In other words, as h>0 we can use the work above to find solutions to this differential equation. We will also go back to x's with using the variable transformation in reverse.

h= - x

Now here we take the real, distinct case first to notice what happens.

m (h) = c₁h^r1 + c₂ h^r2

y(x) = c₁ (-x) ^r1 + c₂ (-x) ^r2

Here, we could do that for the rest of the cases if we needed to, although before doing that let's see that if we recall the definition of absolute value as,

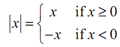
We can combine both of our solutions to such case in one and write the solution,

y(x) = c₁ |x| ^r1 + c₂ |x| ^r2

x ≠ 0;

Remember that we still require to avoid x=0 as we could even get division by zero. Though it is now a solution for any interval which doesn't have x=0.

We can do similarly for the other two cases and the subsequent solutions for any interval not having x=0.

y(x) = c₁ |x|^r + c₂ |x|^r In|x|

y(x) = c₁ |x|^l (cos m In|x|) + c₂ |x|^l (sin m In|x|)

We can create one more generalization before working one more illustration. A more common form of an Euler Equation is as,

a(x - x₀)² y'' + b (x - x₀) y' + cy = 0;

And we can ask for solutions for any interval not having x = x₀. The work for generating the solutions in that case is identical to all the above work and therefore isn't demonstrated now.

The solutions for this general case for any interval not containing x=a are,

y(x) = c₁|x - a|^r1 + c₂ |x - a|^r2

y(x) = |x - a|^r (c₁+ c₂  In |x - a|)

y(x) = |x - a|^l c₁ cos (m In|x -a|) + c₂ sin (m In|x - a|)

Here then the roots are for solution to:

ar(r - 1) + b(r) + c = 0