Determine the solution to the subsequent differential equation.

dv/dt = 9.8 - 0.196v

Solution

Initially we require finding out the differential equation in the accurate form.

dv/dt + 0.196v = 9.8

By this we can notice that p(t)=0.196 and so µ(t) is after that:

µ (t) = e^{∫0.196 dt} = e ^0.196t  

Remember that officially there must be a constant of integration in the exponent by the integration. Though, we can drop that for accurately the same purpose which we dropped the k from the (8).

Currently multiply all the terms in the differential equation through the integrating factor and do several simplifications

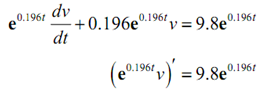
Integrate both sides and remember that the constants of integration that will happen from both integrals.

∫e^0.196t v)' dt = ∫9.8 e^0.196t dt

e^0.196t v + k = 50 e^0.196t + c

This time we have to play with constants again.  We can subtract k from both sides to determine.

e^0.196t v = 50 e^0.196t + c - k

Both c and k are unidentified constants and thus the difference is also an unidentified constant.  We will thus write the difference as c.  Accordingly, we here have  

e^0.196t v = 50 e^0.196t + c

By this point on we will only place one constant of integration down as we integrate both sides identifying that if we had written down one for all integrals, as we must, the two would just end up getting absorbed in each other.

The last step in the solution process is afterward to divide both sides via e^0.196t or to multiply both sides via e^-0.196t.  Either will work, although I generally prefer the multiplication route.  Doing this provides the general solution to the differential equation.

v(t) = 50 + ce^-0.196t

By the solution to this illustration we can now notice why the constant of integration is so significant in this process. Without this, in this case, we would find a single, constant solution, v(t)=50. Along with the constant of integration we find infinitely several solutions, one for all values of c.

Back in the direction field region where we initially derived the differential equation utilized in the last illustration we used the direction field to assist us sketch several solutions. Let's notice if we found them accurate to sketch several solutions all we require to do is to pick various values of c to find a solution. Some of these are demonstrated in the graph below.

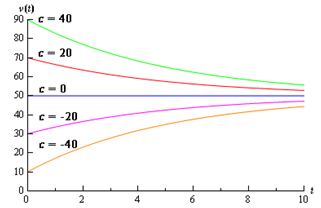
Thus, it seems as we did pretty good sketching the graphs back in the direction field section.

Here, recall from the Definitions section that the first Conditions will permit us to zero in on a specific solution. Solutions to first order differential equations but not just linear like we will notice will have a particular unknown constant in them and thus we will require exactly one initial condition to determine the value of which constant and thus find the solution that we were after. The first condition for first order differential equations will be of the as of form:

Y(t₀) = y₀

Recall also a differential equation with an enough number of initial conditions is termed as an Initial Value Problem (IVP).