Determine the resultant of the system of forces:

Four forces act on a body as illustrated in Figure. Determine the resultant of the system of forces.

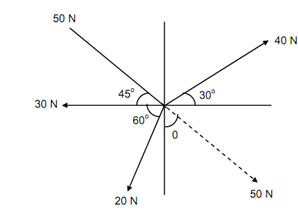
Figure

Solution

Resolving all of forces along x-axis, we attain

 R_x  = ∑ F_x

= F₁ cos θ₁ + F₂ cos θ₂  + F₃ cos θ3 + F₄ cos θ₄

= 40 cos 30^o  + 50 cos 315^o  + 30 cos 180^o  + 20 cos 240^o

Note:  The angle created by 50 N forces is measured in anticlockwise direction from positive x axis after making the force work away from O by principle of transmissibility of the force.

∴ R_x  = 40 cos 30^o  + 50 cos 45^o  - 30 cos 0^o  - 20 cos 60^o

θ ≤ 90^o can be chosen in appropriate quadrant with correct signs as indicated above.

R_x  = 34.64 + 35.36 - 30.00 -10.00

R_x = 30 N

Likewise, resolving all of the forces along y axis, we obtain

R_y = ∑ F_y

= F₁ sin θ₁ + F₂ sin θ₂ + F₃ sin θ₃ + F₄ sin θ₄

= 40 sin 30^o + 50 sin 315^o + 30 sin 180^o + 20 sin 240^o

= 20.00 - 35.36 + 0.00 - 17.32

      R_y = - 32.68 N

Therefore, the resultant in vector form can be expressed as

R¯ = (30 N) i¯ + (- 32.68 N) j¯

The magnitude of the resultant is specified by following

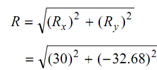
        = 44.36 N

The direction θ may be worked out as,

θ = tan ^-1   (R_y /R_x)

= tan ^-1 (- 32.68/30) = - 47^o 26′ 53′′

= 312^o 33′ 7′′

The resultant contain a magnitude of 44.36 N and is working in IVth quadrant making an angle of 312^o 33′ 7′′ in anticlockwise direction from positive x axis.