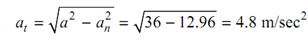Determine the radius of curvature - motion of a particle:
The motion of a particle in XOY plane is defined by the equation
r (t ) = 3t i^ + (4t - 3t 2 ) j^
The distances are in metres. Determine its radius of curvature and its acceleration while it crosses the x axis again.
Solution
We have x = 3t, y = (4t - 3t 2 )
∴ t = x/3 , ∴ y = 4 x/3 - x 2/3
∴ The equation is a second degree curve and if we equate it to zero, we shall get two values of x.
The path crosses the x axis at x = 0, y = 0 and t = 0 second, x = 4, y = 0, t = 4 /3 second as shown in Figure.
The radius of curvature is attained as below.
1/ ρ = ± (d 2 y/ d x 2) / [1+ (dy/dx)2] (3/2)
y = 4 /3 x - x 2 /3
dy / dx = 4/3 - (2/3) x
and
d2 y /dx2= - 2/3
∴ 1/ ρ = ± (2/3) / [ 1+ ((4/3)-(2/3))2](3/2)
at x = 0 or at x = 4 m
∴ 1/ ρ = ± (2/3) / [ 1+ ((4/3) 2](3/2) ∴ 1/ ρ = ± (2/3) / [ 1+ ((-4/3) 2](3/2)
±( 2 /3) /(25/9)(3/2); ±( 2 /3) /(25/9)(3/2)
= 18/125 ; = 18/ 125
ρ = 6.94 m ρ = 6.94 m
We have, x = 3t y = 4t - 3t 2
∴ vx = 3 m / sec ∴ v y = 4 - 6t m/ sec.
∴ for t = 0, vx = 3 m/sec., vy = 4 m/sec.
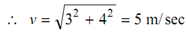
Differentiating further, we obtain
d 2 x/dt2 = ax = 0, d 2 y /dt 2 = a y = - 6
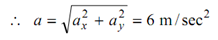
The total acceleration is constant and equal in magnitude to 6 m/sec2.
At both of instants t = 0 and t = 4/3 seconds. The normal acceleration may be found as
a n = v2 / ρ = 25 /6.94 = 3.6 m / sec2
and tangential acceleration