Determine the normal and shear stress elements:

The state of stress at a point is given through the stress components σ_x = 70 MPa, σ_y = 10 MPa, and τ_xy = - 40 MPa. Using Mohr's circle find (i) Principal stresses, and (ii) Principal planes. Also, determine the normal and shear stress elements on planes making 25^o, 40^o and 60^o associatively along with the x plane.

Figure

Solution

(a)        Choose (σ, - τ) coordinate system to a suitable scale.

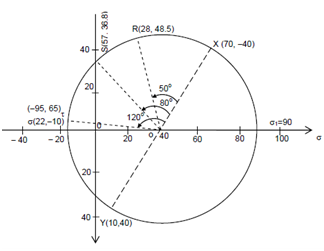
(b)        Mark the points X (70, - 40) and Y (10, + 40).

(c)        Draw a circle with XY as diameter. This circle cuts σ axis at A and B.

(d)        Measure the coordinates of A and B to obtain principal stresses

σ₁  = 90 MPa,  σ₂  = - 10 MPa

(The radius of the Mohr's circle gives τ_max = 50 MPa)

(e)        Measure ∠ XOA ; Here, ∠ XOA = - 52.8^o .

∴          Aspect angle Φ1 of major principal plane is - 26.4^o.

(f)        Measure ∠ XOB ; Here, ∠ XOB = + 127.2^o

∴          Aspect angle Φ2 of major principal plane is + 63.6^o.

(g)        Draw radial lines OR, OS and OT making angles 50^o, 80^o and 120^o with OX.

(h)        Coordinates of R give the normal and shear stress components on the plane which makes 25^o with the x plane. Here,

σ_n  = 28 MPa, τ_nt  = - 48.5 MPa

(i)         Coordinates of S given the normal and shear stress components on the plane which aspect angle 40^o. Here,

σ_n  = 5.7 MPa, τ_nt  = - 36.8 MPa

(j)         Coordinates of T give the normal and shear stress components on the plane with aspect angle 60^o. Here,

σⁿ  = - 9.5 MPa, τ^nt  = - 6.5 MPa