Determine the Measurements of Segments and Angles

Postulate 1.5 (The Distance Postulate)

There is a unique positive number corresponding to every pair of points.

Postulate 1.6 (The Ruler Postulate)

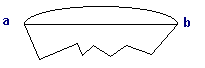
The points on a line are in a one-to-one correspondence with the real numbers, so that number differences measure distances. The term distance in geometry is always interpreted as the shortest path between two points.

The shortest path is represented by the segment joining the points rather than any zigzag or other type of route.

1. Measuring Segments

We can measure segments using rulers. Inches, feet, yards, or meters are commonly used as units of measure. We use the symbol “mAB¯” to represent the distance or measure between the endpoints A and B.

2. Measuring Angles

When two lines intersect, angles are formed. More than four thousand years ago, the ancient Babylonians chose 360 as their basis to measure angles. The unit of measurement of an angle is called the degree(°). The size of an angle is the amount of turning you would do if you were at the vertex. If you continued rotating and turned all the way around to your starting point, you would have turned 360°. This means the measure of one rotation is 360°.

The measure of an angle can be expressed in different ways. We can speak of an angle whose measure is negative or whose measure is greater than 360°.

Each degree(°)of an angle is divided into 60 minutes('), 1° = 60'.
Each minute is divided into 60 seconds("), 1' = 60".
Thus 30.25° = 30° 15', 70.6° = 70° 36', 1.5' = 1' 30".
Usually, we use a protractor to measure angles. 
Postulate 1.7 (The Angle Measure Postulate)
There is a unique number between 0 and 360 corresponding to every angle.            
The number is called the measure of the angle.
We use "m?A" to denote the measure of ?A.

Postulate 1.8 (The Protractor Postulate)

There is a one-to-one correspondence between the rays in a half-rotation and the real numbers from 0 to 180 inclusive, so that number differences measure angles.

Definition 1.11

Segments or angles are congruent if they have the same measure.
We use the symbol "≅" to denote congruence for segments and angles.

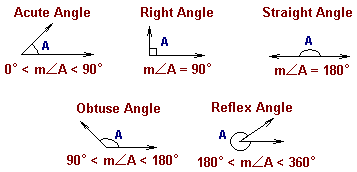
Naming of angles

An acute angle is an angle whose measure is greater than 0° and less than 90°.
A right angle is an angle whose measure is 90°.
An obtuse angle is an angle whose measure is greater than 90° and less than 180°.
A straight angle is an angle formed by a line and whose measure is 180°.
A reflex angle is an angle whose measure is greater than 180° and less than 360°.