Determine the loading on the beam:

Shear force diagram for a loaded beam is illustrated in Figure. Determine the loading on the beam & therefore, draw the bending moment diagram. Situate the point of contraflexure, if any.

Solution

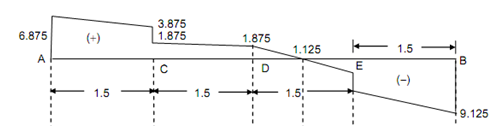
Let us analyse the shear force diagram specified in given Figure .

At A

The shear force diagram enhance suddenly from 0 to 6.875 kN in upward direction, at A. This denote that there is support at A, along magnitude of reaction 6.875 kN.

Between A and C

The SF diagram is an inclined straight line among A and C. It denotes that there is a uniformly distributed load among A and C. The load enhance from 6.875 kN to 3.875 kN (6.875 kN - 3.875 kN = 3 kN). Therefore, the beam carries a uniformly distributed load of   3/1.5= 2 kN/m among A and C.

At C

The shear force diagram suddenly reduces from 3.875 kN to 1.875 kN. It denote that there is a point load of 2 kN (3.875 kN - 1.875 kN) working in downward direction at C.

Figure

Between C and D

As the shear force diagram is horizontal among C and D, there is no load among C and D.

Between D and E

The SF diagram is an inclined straight line among D and E. It denotes that there is a uniformly distributed load. Load reduction from + 1.875 kN to - 1.125 kN. Thus, the beam carries a uniformly distributed load of (+1.875 + 1.125 = 3 kN) ⇒ 3/1.5= 2 kN/m between D and E.

At E

 The shear force diagram has sudden reduce from - 1.125 kN to - 6.125 kN. It denotes that there is a point load of 5 kN (↓) at E.

Between E and B

The SFD reduce from - 6.125 kN to - 9.125 kN by an inclined straight line, that shows that the beam carries a u.d.l. of   3 /1.5 = 2 kN/m among E and B.

At B

As there is a sudden enhance from - 9.125 kN to 0 at B, there is a support at B of reaction 9.125 kN.

Bending Moment

BM at A,         M_A = 0

BM at C,           M _C    = (6.875 × 1.5) - (2 × 1.5 × (1.5/2) )  = 8.06 kN^-m

BM at D ,  M _D  = (6.875 × 3) - 2 × 1.5 × 2.25 = (- 2 × 1.5) = 10.875 kN-m

BM at E,  M _E  = (9.125 × 1.5) - ( 2 × 1.5 × (1.5/2)   = 11.44 kN-m

Maximum Bending Moment

Let a section XX among D and E at a distance x from the end B. SF at section XX,

F_x  =- 9.125 + 5 + 2 x - 4.125 + 2 x = 0

∴ x = 2.0625 m  (for maximum BM)

∴ M _max            = (9.125 × 2.0625) - 5 × (2.0625 - 1.5) - ( 2 × 2.0625 × (2.0625/2) )

= 11.75 kN-m