Storm water flows at a depth of 4 ft in the natural channel as shown in the figure. The channel has a slope of 0.0l ft/ft and n = 0.025.

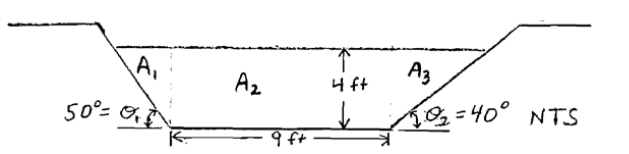
1. Determine the flow area:

    Area 1: Tan σ¹ = opp/adj      adj = opp/Tan σ¹       adj = 4/1.19 = 3.36 ft

               (1/2)(b)(h) = (1/2)(3.36)(4) = 6.7 ft²

     Area 2 = (b)(h) = (9)(4) = 36 ft²

    Area 3 = Tan σ² = opp/adj      adj = opp/Tan σ²     adj = 4/0.84 = 4.76 ft

                 (1/2)(b)(h) = (1/2)( 4.76)( 4) = 9.5 ft²  

    Total Area= Area 1 +Area 2 +Area 3 = 6.7 ft² + 36 ft² + 9.5 ft² = 52 ft²2. 

2. Determine the flow velocity:  

v = (1.49/n) (R)^0.67 (S)^0.5       R = A/P      P_total = P_{Area 1} + P_{Area 2} + P_{Area 3}

P_{Area 1} = hyp_{Area 1}    sin σ₁ = opp_{Area 1} /hyp_{Area 1}      hypArea 1 = 4/sin σ₁ = 5.2 ft

P_{Area 3}= hyp_{Area 3}    sin σ₂ = opp_{Area 3} /hyp_{Area 3}      hyp_{Area 3} = 4/ sin σ₁ = 6.2 ft

    P = P_{Area 1} + P_{Area 2}  P_{Area 3} = 5.2 ft + 9 ft + 6.2 ft = 20.4 ft

    R = A/P = 52 ft² / 20.4 ft = 2.5 ft

    v = (1.49/0.025)(2.5)^0.67 (0.01)^0.5 = (59.6)(1.88)(0.1) = 11.2 ft/sec

3. Determine the flow rate:    Q = vA = (11.2 ft/sec)(52 ft²) = 582 ft³/sec  

4. Determine the hydraulic grade line (HGL) at this channel section:  

    The hydraulic grade line is the depth of flow HGL = 4 ft  

5. Determine the energy grade line (EGL) at this channel section:  

    P/γ = 4ft    Z = 0 ft (bottom)    v²/2g = (11.2)²/64.4 = 1.95 ft

    EGL = 4ft + 0 ft + 1.95 ft = 5.95 ft