Determine the example of Future Value of an Annuity

An annual payment of 7000 $ is invested at 5% per annum compounded yearly. What will be the amount after 20 years?

Solution

Here i = 0.05, P = 7000, and n = 20. Putting it in the formula we get:

Future Value = 7000{[(1+ 0.005)²⁰ -1]/0.05}

FV = 7000 x 33.066 = 2,31,462 $

We have taken a shortcut here.  We looked at future value of 1$ at the end of 20 years at 5% interest in the Future Value Annuity Factor Table (i.e. find the value of Future Value Annuity Factor n, i) and found figure to be 33.066 (try finding the figure yourself) and then substituted figure here to get the answer. Another way of doing it would be to use a scientific calculator and calculate the value which comes out to be same.

Let's see how we use Microsoft Excel to do the same. Insert values as given in the illustration. Here r = I = 0.05, Nper is the number of periods = 20, Pmt is periodic annuity = 7000. Pv is the present value = 0 in this case as it an annuity and Type is a value representing the timing of payment = 0 in this case as first investment is done at the end of the period 1. Note that in earlier case this also means that we get returns at the end of the period 20 simultaneously when we make last payment. Putting these values we get the below screen.

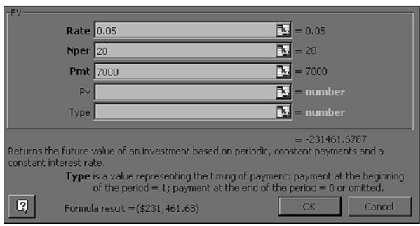
Can you find answer?  Yes, it's 231,461.68 $ a difference of 0.32 $ from the answer we got using table above.

A variation on this would be that payment made at the start of the period rather than the end of the period. This means that you earn extra interest for one year. Formula is slightly different in that whole value is multiplied by (1+i) resulting in the below formula:

Future Value= A {[(1+i) ⁿ -1]/i} (1+i)

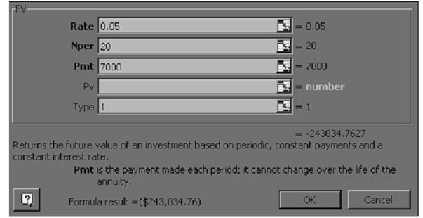
In excel spreadsheet we just have to change the type to 1 to get desired result.

Result now comes to 243,034.76 $, which is nothing though earlier figure of the result now comes to 2, 43,034.76 $, which is nothing but earlier figure of 2, 31,461.68$ multiplied by 1.05 (i.e. 1+i).

Yet this leaves one problem unanswered: If projects have different time spans (which could be as far apart as 50 years or more) how do we use results that we get from here to compare. It becomes much difficult. Also we can't be too sure of the discounting rates and cash flows so getting comparable values will be difficult to say the least.  To solve this problem we solve for present value.