Determine the equation of the plane that consists of the points P = (1, -2, 0), Q = (3, 1, 4) and R = (0, -1, 2).

Solution

To write down the equation of plane there is a requirement of a point (we've got three thus we're cool there) and a normal vector.  We need to find out a normal vector. Remind however, that we saw how to do this in the Cross Product section.

We can form the following two vectors from the specified points.

^→PQ = (2, 3, 4)

 ^→PR = (-1,1, 2)

 These two vectors will lie totally in the plane as we formed them from points that were in the plane. 

Notice also that there are several possible vectors to use here; we just select two of the possibilities.

Here now, we are be familiar with that the cross product of two vectors will be orthogonal to both of these vectors. As both of these are in the plane any vector that is orthogonal to both of these will as well be orthogonal to the plane. Hence, we can make use of the cross product as the normal vector.

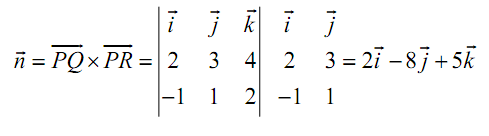
After that the equation of the plane is,

2 (x-1) - 8 (y+2) + 5 (z-0) = 0

2x - 8y + 5z = 18

Now we used P for the point, however could have used any of the three points.