Determine the eigenvalues and eigenvectors of the subsequent matrix.

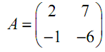
Solution:

The first thing that we require to do is determine the eigen-values. It means we require the next matrix,

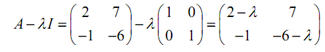
In particular we require determining where the determinant of this matrix is zero.

det(A - lI_n)= (2 -l)(-6 -l) + 7 = = l² + 4l + 5 = (l +5) (l-1)

Therefore, this looks like we will have two easy eigenvalues for this matrix, l₁=-5 and l₂=1.

We will now require finding the eigenvectors for each of these. Also see that as per the fact above, the two eigenvectors must be linearly independent.

To get the eigenvectors we simply plug into all eigenvalues in (2) and solve. Therefore, let's do that.

l₁=-5;

In this case we require solving the following system,

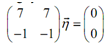
Recall that formally to solve this system we utilize the subsequent augmented matrix.

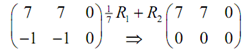
Upon reducing down we notice that we find a single equation,

7h₁ + 7h₂ = 0                           ⇒         h₁ = h₂                        

It will yield an infinite number of solutions. It is expected behavior. By recall that we picked the eigenvalues hence the matrix would be particular and thus we would find infinitely many solutions.

Remember as well that we could have known this from the original system. It won't always be the case, although in the 2x2 case we can notice from the system that one row will be a multiple of another and so we will determine infinite solutions. From that point on we won't be in fact solving systems in these cases.  We will simply go straight to the equation and we can utilize either of the two rows for this equation.

Here, let's get back to the eigenvector, as it is what we were after. Generally, then the eigenvector will be any vector which satisfies the following,

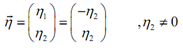
To find this we used the solution to the equation which we found above.

We actually don't need a general eigenvector though so we will pick a value for h₂ to find an exact eigenvector. We can select anything (except h₂ =0), so pick something which will make the eigenvector "nice". Remember as well that as we've already assumed such eigenvector is not zero we should select a value that will not give us zero, that is why we need to ignore h₂ =0 in this case. There is the eigenvector for this eigen-value.

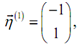
By using h₂ =1.

Now we find to do this all over again for the second eigen-value.

l₂=1.

We'll perform much less work along with this part so we did with the earlier part. We will require solving the following system.

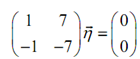
Obviously both rows are multiples of each other and thus we will find infinitely many solutions. We can select to work with either row. We'll run along with the first since to ignore having too various minus signs floating around.  Doing this provides us,

h₁ + 7 h₂ = 0                                        h₁ = - 7 h₂

Remember that we can solve that for either of the two variables. Though, with an eye in directions of working with these later on let's aim to ignore as many fractions as possible. The eigenvector is after that,

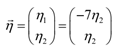
Here h₂ ≠ 0.

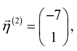
By use of h₁= 1

By summarizes, we get

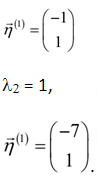
Remember that the two eigenvectors are linearly independent like predicted.