Example: A 16 lb object stretches a spring 8/9 ft by itself. Here is no damping as well as no external forces acting on the system. The spring is firstly displaced 6 inches upwards from its equilibrium position and specified an initial velocity of 1 ft/sec downward. Determine the displacement at any time t, u(t).

Solution

We first require setting up the IVP for the problem. It needs us to get our hands on m and k.

It is the British system so we'll require calculating the mass.

m = W/g = 16/32 = ½

Here, let's get k. We can use the fact that mg = kL to determine k. keep in mind that we'll need all of our length units similar. We'll utilize feet for the unit of measurement for this problem.

k = (mg)/L = 16/(8/9) = 18

For the initial conditions recall that upward motion/displacement is negative whereas downward motion/displacement is positive. Also, as we decided to do everything in feet we had to change the initial displacement to feet.

Here, to solve it we can either go by the characteristic equation or we can just jump straight to the formula which we derived above. We'll do it that manner. First, we require the natural frequency,

w₀ = √(18/(1/2)) =√ (36) = 6

The general solution, with its derivative, is after that,

u (t ) = c₁ cos (6t)+ c₂ sin (6t)

u′ (t ) = -6c₁ sin (6t )+6c₂ cos (6t )

Applying the initial conditions provides,

-1/2 = u(0) = c₁,           c₂ = -1/2

1 = u'(0) = 6c₂cos(6t),             c₂= 1/6

The displacement at any time t is after that,

u(t) = -1/2cos(6t) + 1/6 sin(6t)

Here, let's convert this to a particular cosine. Firstly let's find the amplitude, R.

R = √((-(1/2))² + (1/6)²) = √(10)/6 = 0.52705

You can utilize either the accurate value here or a decimal approximation. Frequently the decimal approximation will be simple.

Here let's get the phase shift.

d= tan^-1((1/6)/(1/2))  = -0.32175

We require being careful with this part. The phase angle determined above is in Quadrant IV, although there is also an angle in Quadrant II which would work also. We find this second angle by adding d onto the first angle. Therefore, we actually have two angles. Hence they are,

d₁= -0.32175

d₂= d+ p = 2.81984

We require deciding that of these phase shifts is correct, as only one will be accurate. To do it recall that

c ₁ = R cos(d)

c₂ = R sin(d)

Currently, as we are assuming that R is positive it means that the sign of cosd will be similar as the sign of c₁ and the sign of sind will be similar as the sign of c₂. Therefore, for this specific case we must have cosd < 0 and sind > 0. It means that the phase shift should be in Quadrant II and therefore the second angle is the one which we necessitate

Thus, after all of this the displacement at any time t is,

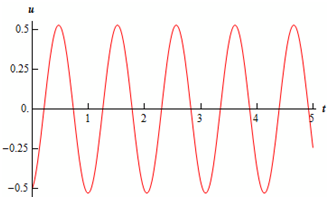
u (t ) =0.52705 cos (6t - 2.81984)

There is a figure out of the displacement for the first 5 seconds.

Here, let's take a look at a slightly more realistic situation. There no vibration will go on forever.  Therefore let's add in a damper and notice what happens now.