Determine the deflection under the loads:

Determine the deflection under the loads as shown in Figure

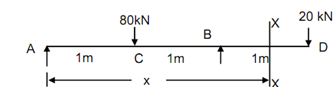
Solution

∑ F_y  = 0, so that R_A + R_B  = 80 + 20 = 100 kN          -------- (1)

Σ M about A = 0.

80 × 1 + 20 × 3 = R_A × 2  ∴ R_B  = 70 kN (↑)

From Eqs. (1) and (2),

R_A = 30 kN ( ↑ )              ------------ . (2)

M = 30 x - 80 ( x - 1) + 70 ( x - 2) -------- (3)

EI (d ² y /dx²) = M = 30 x - 80 [ x - 1] + 70 [ x - 2]         ------------- (4)

EI dy/ dx = 15 x - 40 [ x - 1]² + 35 [ x - 2]² + C₁                   --------- (5)

 EIy = 5 x³  - 40 [ x - 1]³  + 35 [ x - 2]³  + C x + C      --------- (6)

The boundary conditions are :

 At A, x = 0,     y = 0                               -------- (7)

At B, x = 2 m,    y = 0                    -------- (8)

From Eq. (6) and (7), C₂ = 0

From Eqs. (6) and (8)

0 = 5 × 2³  - 40 [2 - 1]³  + C₁  × 2

C₁  =- 40 /3

∴          EIy = 5 x³ - (40/3) [ x - 1]³  + (35/3) [ x - 2]³  - (40/3) x        . . . (7)

Deflection at C,

x = 1 m

EIyC      = 5 × 1³  - (40/3) × 1 = - 25/3

∴          y_C = - 25 /3 EI                    --------------- (8)

Deflection at D,

x = 3 m

EIy _D     = 5 × 3³  - (40 /3)(3 - 1)³  + 35 (3 - 2)³  - (40 /3)× 3 = 0

Y_D= 0