Determine the angle of twist - solid steel shaft:

A solid steel shaft 6 m long is fixed at each of the end. A torque of 3 kN-m is applied to the shaft at a section 2 m from one end. What is the fixing torques developing on the ends of the bar? If the shaft diameter is equal to 40 mm, what are the maximum stresses in two positions? Also determine the angle of twist where torque is applied.

Take E = 80 GPa.

Solution

E = 80 GPa = 0.8 × 1011 N/mm2

T = 3 kN-m

d = 40 mm = 0.04 m

J =  (π /32 )d 4 = (π /32)× (0.04)⁴  = 2.5 × 10^{- 7} m⁴

R = 40/2 = 20 mm = 0.02 m⁴

Z _P        = J/ R = 1.26 × 10^{- 5} m³

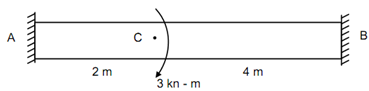
Portion AC

T₁ = torque

θ₁ = (T₁ l₁ / GJ ) = 2T₁ / G J

τ_max      = (T₁ /J ) R =  T₁ / Z _P

Portion CB

θ₂ = T₂  l₂/ GJ  = 4T₂ / GJ

t_max = (T₂ /J ) R =  T₂ / Z _P

∴          T₁  + T₂  = 3

T₂  = (3 - T₁ )

θ₁ = θ₂                                          ---------- (1)

⇒         2T₁/ GJ = 4T₂/GJ

T₂  = 2T₂               -----------------(2)

 (1) and (2),

2T₂  + T₂  = 3

⇒ T₂  = 1 kN-m --------- (3)

T₁  = 2T₂  = 2 × 1 = 2 kN-m     -------- (4)

Maximum Stresses

Portion AC

τ_max = (2 × 10³) / (1.26 × 10^{- 5}) = 159 × 10⁶ N/m2  = 159 N/mm²

 Portion CB

τ_max = (1 × 10³) / (1.26 × 10^{- 5})

 = 80 × 10⁶ N/m²  = 80 N/mm²

 Angle of twist :

θ= 2T₁ /GJ

=(2 × (2 × 10³ )) / ((0.8 × 10¹¹ ) (2.5 × 10^{- 7} )) = 2 × 10^-1 radian = 0.2 radians