You are gambling. There is a white urn in front of you, which contains a total of 100 black and white balls. You are blindfolded, get to pick one ball randomly, and see which color you picked. If your ball is black, your X₁ is 0. If your ball is white, your X₁ is 1. Once your X₁ is determined, you proceed to the second level. In the second level, there are two urns: red and blue. In each urn are there 100 black and white balls again but at different ratios. If your X₁ is 0, you will pick a ball from the red urn and if your X₁ is 1 you will pick a ball from the blue urn. If your ball in the second level is white, your X₂ is 1. If it is black, your X₂ is 0.

In each urn are there 100 balls. Out of 100 balls: 100  p are white in the white urn: 100  q are white in the red urn: 100  r are white in the blue urn, for p, q, r ∈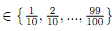

There are two types of gambles. The first type (G1) is you get $M₁ X # of white balls you picked. The second type(G₂) is you get $M₂ if you picked a white ball from the first level and $M₃ if you picked a white ball from the second level. You need to pay $C₁ to do the first type and $C₂ to do the second type. Let Y₁ be the net amount of the money you will earn if you do the G₁ and Y₂ be the net amount of money you will earn if you do the G₂.

(a) Let X =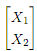. What is Supp (X)? For x = 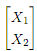∈ Supp (X), let fX (x) = Pr [X = x] and FX (x) = Pr [X₁ ≤ x₁;X₂ ≤ x₂]. Write down fX (x) and FX (x) for all x ∈ Supp (X).

(b) It is possible to write E [X₂]X₁ = x] = β₀ + β ₁x. Write β₀ and β ₁ with respect to p, q, and/or r:

(c) Let Y = 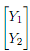. The Y can be written as Y = AX + b for a A ∈ R^2x2 and a b ∈ R². What are A and b? Let E [X] = μX ∈ R² and V [X] = X ∈ R^2x2 . Write E [Y ] and V [X] with respect to μx , ∑ , A, and b.