Determine load carried by each cylinder:

A hollow steel cylinder of cross-sectional area 2000 mm² concentrically surrounds a solid aluminium cylinder of cross-sectional area 6000 mm². Both cylinders have the same length of 500 mm before a rigid block weighing 200 kN is applied at 20^oC as shown in Figure. Determine

(a) The load carried by each cylinder at 60^oC.

(b) The temperature rise required for the entire load to be carried by the aluminium cylinder alone.

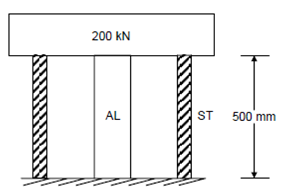
Figure

For computation purposes, take following values :

E_steel = 210 GN/m² and E_aluminium = 70 GN/m²

σ_steel = 12 × 10^{- 6} K^-1 and α_aluminium = 23 × 10^{- 6} K^-1

Figure shows the free thermal expansions Δ_a and Δ_s together with the common expansion Δ under the load of 200 kN (the subscripts a and s standing for aluminium and steel respectively).

For a temperature rise of ΔT K,

We have,

Δ_a = 500 × 23 × 10^-6 × ΔT = 11.5 × 10^-3 ΔT mm

Δ_s = 500 × 12 × 10^-6 × ΔT = 6 × 10^-3 ΔT mm

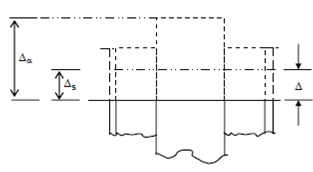
Under load, the strains are

ε_α   = Δ_a  -Δ /500

and  ε_σ  = Δ_s  -Δ /500         

and the corresponding stresses are as follows :

σ_α =70 × 10³/500 (Δ_α  - Δ) = 140 (Δ_α  - Δ) N mm^-2

σ_s = 210 × 10³/500   (Δ_s - Δ) = 420 (Δ_s - Δ) N mm^-2

For equilibrium of vertical forces,

σ_a  × 6000 + σ_s  × 2000 = 200 × 10³  N

Substituting for σ_a, σ_s, Δ_a and Δ_s, we get

(11.5 × 10^{- 3} × ΔT - Δ) + (6 × 10^-3 ΔT - Δ) = 5/21

Hence,

Δ= 8.75 × 10^-3 ΔT - 5/42

The loads taken by the aluminium and the steel are therefore,

P_a  = σ_a  × 6000 N

= 840 ( 2.75 × 10^-3  ΔT +5/42)  kN

P_s  = σ_s  × 2000 N

= 840  ((5/42) - 2.75 × 10^{- 3}  ΔT) kN

These equations will be valid as long as Δ is less than Δ_s. the load will be completely carried by aluminium when Δ_s becomes equal to Δ.

(a)        at 60^oC,

ΔT = 60 - 20 = 40 K

P_α  = 840 ( 2.75 × 40 × 10^-3  +5/42)

= 192.4 kN

P_s  = 200 - 192.4 = 7.6 kN

(b)       The load will be carried completely by aluminium when

6 × 10^-3 × ΔT = 8.75 × 10^{- 3} × ΔT - 5/42

or        ΔT = 5 × 10³/2.75 × 42 = 43.3^o C

i.e. at a temperature of (20 + 43.3) = 63.3^oC.