Determination of Reaction at the Support beam:

Draw a SFD & BMD for the beam illustrated in Figure

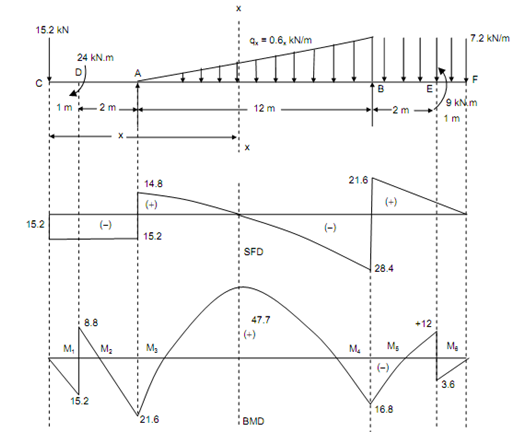
Figure

Solution

Determination of Reaction at the Support B

Letting left side, take moments around A,

R _B   × 12 - 7.2 × 3 × (12 + (3/2) )+ 15.6 - ((1/2) × 12 × 7.2 × (2/3) × 12 ) = M

M _A = 12 R_B  - 621.6

Letting right side, take moments around A,

M _A  = - (15.2 × 3) + 24 = - 21.6 kN-m

Equating these two equations,

12 R_B  - 621.6 = - 21.6

12 R_B  = 600

R_B  = 50 kN

∴          R _A  = 15.2 + ((½) × 12 × 7.2 ) + (7.2 × 3) - R_B = 80 - 50 = 30 kN

Shear Force (Starting from the Left End A)

 SF at C, F_C  = - 15.2 kN

SF just left of A, F_A  = - 15.2 kN

SF just right of A, F_A  = - 15.2 + 30 = + 14.8 kN

SF just left of B, F _B   = + 14.8 - ( (1/2) × 12 × 7.2 ) =- 28.4 kN

SF just right of B, F_B  =- 28.4 + 50 =+ 21.6 kN

SF at F,   F_F   =+ 21.6 - (7.2 × 3) = 0

Bending Moment (beginning from the Right End F)

BM at F,          M_F = 0

BM just right of E, M E =- ( 7.2 × 1 ×( ½) )  = - 3.6 kN-m

BM just left of E,  M _E  = - 3.6 + 15.6 = + 12 kN-m

BM at B, M _B  = (7.2/2) × 3 × 3 ) + 15.6 = - 16.8 kN-m

BM at A, M _A =- (15.2 × 3) + 24 =- 21.6 kN-m  (considering left side)

BM at C,         M_C = 0

 BM just left of D, M _D = - 15.2 × 1 = - 15.2 kN-m

BM just right of D, M _D  = - 15.2 + 24 = + 8.8 kN-m