What are synchronous counters? Design a Mod-5 synchronous counter using J-K Flip-Flops.
Ans.
Synchronous Counters: It means that all flip-flops are clocked concurrently. The clock pulses drive the clock input of each flip-flop together hence there is no propagation delay.
Mod-5 Counter Synchronous Counter: This have five counter states. The counter design table for such counter shows the three flip-flop and their states also (0 to 5 states), as in table (a), the 6 inputs needed for the three flip-flops. The flip-flop inputs needed to step up the counter from the current to the next state have been worked out along with the assist of the excitation table illustrated in the table.
|
Input
pulse
Count
|
Counter States
A B C
|
Flip-Flop Inputs
|
|
JA KA
|
JB KB JC KC
|
|
0
|
0 0 0
|
1 X
|
0 X 0 X
|
|
1
|
1 0 0
|
X 1
|
1 X 0 X
|
|
2
|
0 1 0
|
1 X
|
X 0 0 X
|
|
3
|
1 1 0
|
X 1
|
X 1 1 X
|
|
4
|
0 0 1
|
0 X
|
0 X X 1
|
|
5(0)
|
0 0 0
|
|
|
Table (a) counter Design Table for Mod-5 Counter
A flip-flop: The first state is 0. This change to 1 after the clock pulses. Thus JA must be 1 and KA may be 0 or 1 (i.e. X ).
B flip-flop: The first state is 0 and this keeps unchanged after the clock pulse. Thus JB must be 0 and KB may be 0 or 1 (i.e. X)
C flip-flop: The state keeps unchanged. Thus Jc must be 0 and KC must be X. The flip-flop input values are entered in Karnaugh maps demonstrated in Table (b) [(i) (ii) (iii) (iv) (v) and (vi)] and a boolean expression is determined for the inputs to the 3-flip-flops and after that each expression is simplified. All the counter states have not been utilized; X's (don't) are entered to indicate un-utilized states. For each input the simplified expressions demonstrated under each map. At last, these minimal expressions for the flip-flop inputs are utilized to illustrate a logic diagram for the counter that is demonstrated in fig. (b).
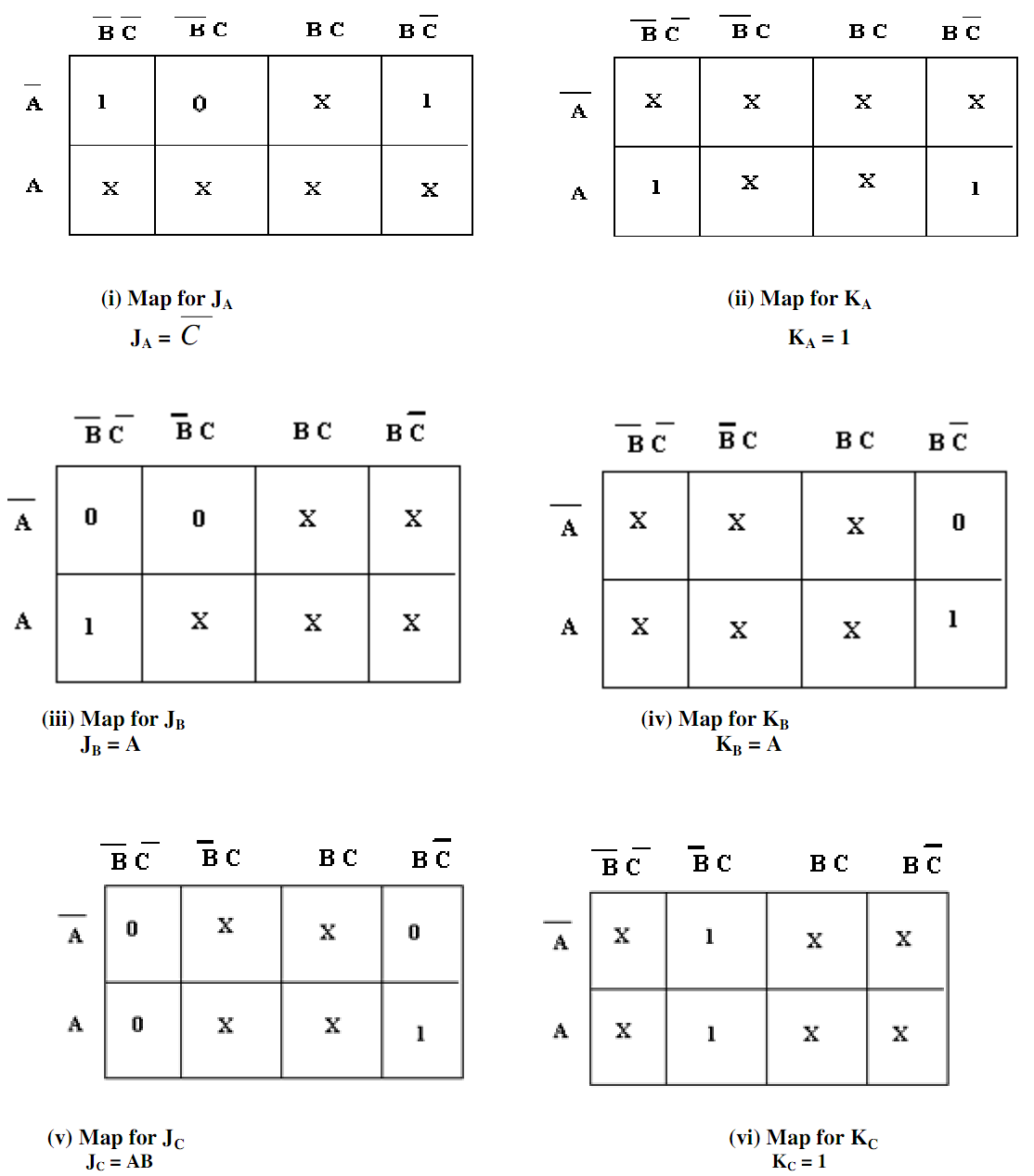
Table (b) Karnaugh Maps for MOD-5 Synchronous Counter
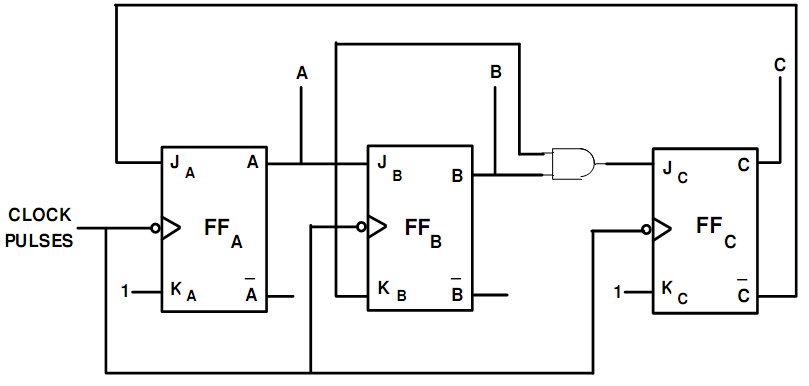
Fig. (b) Logic Diagram of MOD-5 Synchronous Counter