Design a 8 to 1 multiplexer by using the fourvariable function given by
F(A, B, C, D) = ∑ m(0,1,3,4,8,9,15).

Ans. Design of 8 to 1 Multiplexer: It is a four-variable function and thus we require a multiplexer along with three selection lines and 8 inputs. We select to apply variables B, C, and D for the selection lines. It is shown in Table no.1. The first half of given minterms are associated with A' and the second half with A. Through circling the minterms of the function and applying the rules for determine values for the multiplexer inputs, the implementation represented in Table no.2.
The specified function can be implemented along with a 8-to-1 multiplexer as represented in fig.(a). 3 of the variables as B, C and D are applied to the selection lines in order that is B is connected to s2, C to s1 and D to s0.  Hence the inputs of the multiplexer are 0, 1, A and A'. As BCD = 000,001 and 111 output F = 1 because I0 and I8 = 1 for BCD(000), I1 = 1and I9 =1 correspondingly. Thus, minterms m0 = A' B' C' m1 = A' B' C, m8 = A', B', C' and m9 = A' B' C generate a 1 output. While BCD = 010, 101 and 110, output F = 0, as I2, I5 and I6 respectively are equivalent to 0.

Table no.1 Truth Table for 8-1 Multiplexer

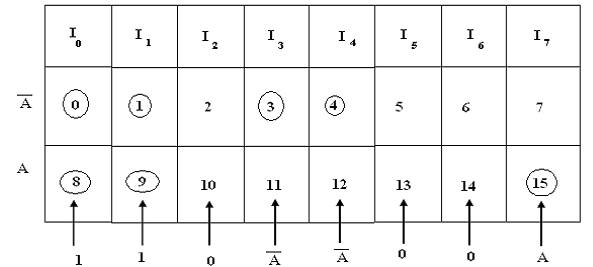
Table no.2 Implementation Table for 8 to 1 MUX

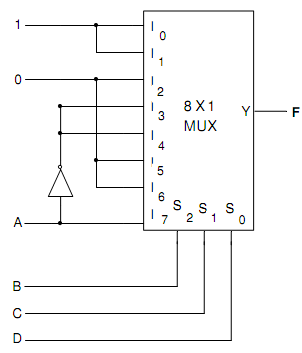
Fig.(a) Logic circuit for 8-to-1 Multiplexer