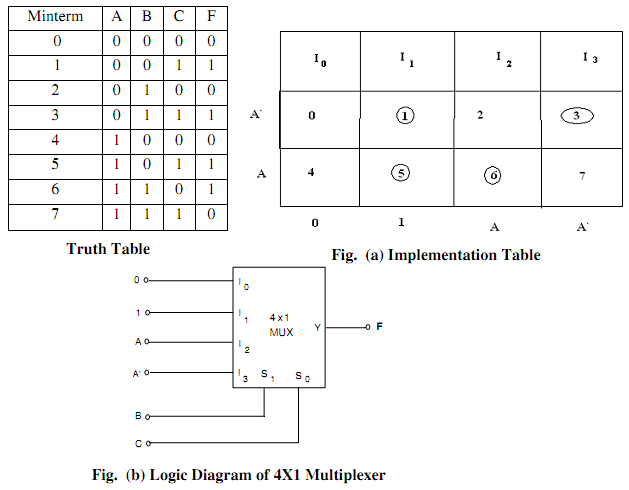
Design a 4 to 1 Multiplexer by using the three variable function given by F(A, B, C) = ∑ m(1,3,5,6)

Ans. The given function F(A,B,C) = ∑ m(1,3,5,6) can be implemented along with a 4-to-1 multiplexer as Demonstrated in Fig.(a). Two of the variables that is, B and C are applied to the selection lines in order, that is B is connected to S1 and C connected to S₀. The inputs of the multiplexer are as 0, I, A, and A'. As I₀ = 0 when BC = 00, output F = 0. Thus, both minterms m₀ = A' B' C' and m4 = A B' C' make a₀ output, because the output is 0 while BC = 00 regardless of the value of A.
As I₁ = 1 when BC = 01, output F = 1. Thus, both minterms m₁ =A' B'C and m₅ = AB'C make a 1 output, as the output is 1. While BC = 01 regardless of the value of A.
While BC = 10, input I₂  is selected. As A is connected to such input, the output will be equivalent to 1 only for minterm m₆ = ABC', although not for minterm m₂ = A' BC', since when A' = I, so A = 0, and as I₂ = 0, we have F = 0. At last, when BC = 11, input I₃ is selected. Because A' is connected to this input, the output will be equivalent to 1 only for minterm m₃ = A' BC, although not for m₇ = ABC. It is given in the Truth Table illustrated  in Table.