QUESTION 1:

(a) Define what you understand by the following terms in Network Flows:

i) UnDirected Path
ii) Directed Path
iii) Directed Cycle.
iv) Tree

In each of the above, show the differences in terms of nodes and directions.

(b) In Radix Heap Algorithm, the technique of buckets is employed. However this idea is an extension of Dial's Algorithm. Analyse the complexity of Radix Heap Algorithm referring to:

1. Movement of nodes between buckets
2. Node Selection principle

QUESTION 2:

(a) Below is the algorithm of a flow decomposition algorithm.

begin
Initialize
while y ≠ Φ do
begin
              Select(s, y)
              Search(s, y)
              if a cycle C is found then do
              begin
                            let D = Capacity(C, y)
                            Add Flow(D, C) to cycle flows
                            Subtract Flow(D, C) from y.
              end
              if a path P is found then do
              begin
                           let D = Capacity(P, y)
                           Add Flow(D, P) to path flows
                           Subtract Flow(D, P) from y.
               end
end

Describe the complexity of the following:

i) Selecting the initial node,
ii) Finding a cycle or a path,
iii) Update step.

(b) Explain how Lower Bounds on Arc Flows are eliminated. Show your workings by a mathematical representation or otherwise.

(c) Refer to the diagram below, show how we could always provide a flow of at most 10 on Node 4.

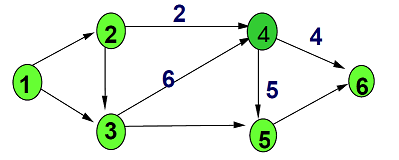
QUESTION 3:

(a) Briefly describe the steps involved in Network Simplex Method.

(b) Referring to Dial's Algorithm and assuming C, to be the Largest arc length, complete the table below.

Variables                                   Cost Value
Number of buckets needed
Time to create buckets.
Time to update d() and
buckets.
Time to find min.
Total running time.

(c) Using Kruskal's algorithm, find the minimum spanning tree of the graph as show in Figure 3.1.

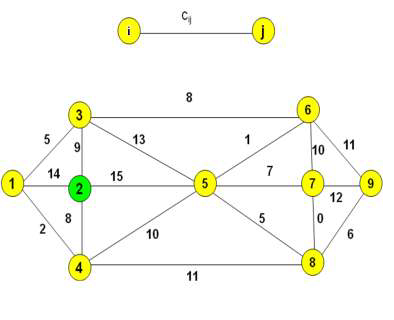
                                                       Figure 3.1

(d) Give mathematical models for the 0-1 knapsack problem and the bounded knapsack problem in Dynamic Programming.

QUESTION 4:

(a) Write down a Generic Label Correcting Algorithm.

(b) Explain how you could detect Negative Cost Cycles in a given set of flows.

(c) Prove that a Negative Cycle Algorithm terminates with an optimal flow.