In mechanics, stress is a measure of the internal forces acting within a deformable body. Quantitatively, it is a measure of the average force per unit area of a surface within the body on which internal forces act. These internal forces are produced between the particles in the body as a reaction to external forces applied on the body. In materials without microstructure (these are materials whose microstructure does not play an important role in the mechanical deformation), these internal forces are distributed continuously within the volume of the material body, and result in deformation of the body's shape. Beyond certain limits of material strength, this can lead to a permanent change of shape or physical failure. The dimension of stress is that of pressure, and therefore the SI unit for stress is the pascal (Pa).

A three-dimensional stress eld in a material can be represented as a symmetric matrix of the following form:

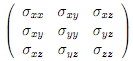
where the diagonal terms represent tensile or compressive stresses and the o-diagonal terms represent shear stresses. At every point in a stressed body there are at least three planes, called principal planes, with normal vectors called principal directions, where there are no normal shear stresses. The three stresses normal to these principal planes are called principal stresses and they are the eigenvalues of matrix (1).

To nd the principal stresses, it is necessary to construct the the following algebraic equation:

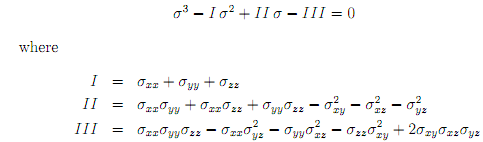
are known as the stress invariants. The roots of equation (2), 1; 2; 3, are the principal stresses.

We consider now a homogeneous material whose stress eld (in MPa) has been found experimentally to be:

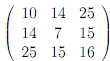
We are interested in nding the principal stresses 1; 2; 3 corresponding to the given stress eld.

1. Find 1; 2; 3 using the following root-nding techniques for solving equation (2): bisection, Newton-Raphson and secant.

2. Show the pseudocode and flowchart for one of the methods.

3. Write a C++ program(s) for all three methods and compare the results.