Q. Describe Laws of Cosines?

The law of cosines is used to find the missing piece of a triangle if we are given either

1. Two sides and the included angle (SAS) or 
2. All three sides (SSS) of the triangle  

All three of the equations say the same thing,   

We can derive the law of cosines for the first equation.  If you want to derive the law for the other equations, simply re-label the vertices and sides of the triangle.  

Begin by drawing a triangle in the first quadrant of a regular graph (rectangular system)  

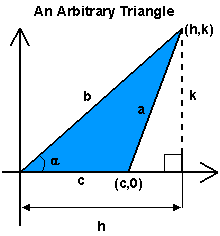
Next, find the length of side a by calculating the distance between (h, k) and (c, 0).

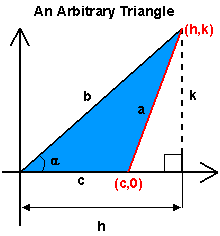
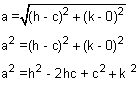
On a different note, looking at the arbitrary triangle we can see that the lines b, h and k form a right triangle.  

  Using the Pythagorean theorem.

b² = h² + k²

 Substitute into the equation for h² + k².

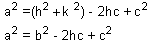
Look at the triangle critically, using the definition of cosine.

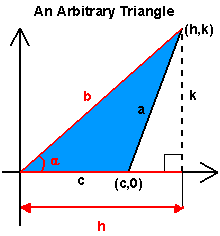
Notice that cos α = h/b

Rearrange to get b cos α = h and substitute back into the equation and rearrange to get

a² = b² + c² -2bc cosα