Q. Describe about full adder?

Let's take full adder. For this other variable carry from previous bit addition is added let'us call it 'p'. Truth table and K-Map for this is displayed in figure below.

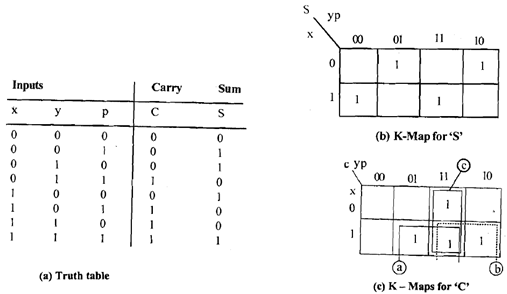
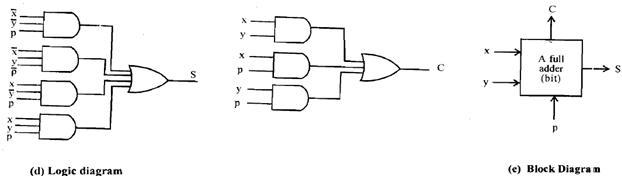
Figure: Full-adder implementation

Three adjacencies marked a,b,c in K-Map of 'C' are

a)

x  y¯  p  + x y p 

  =   x p ( y +  y¯ ) 

  =   x p 

b)

x y p  + x y  p¯ 

  =   x y

c)

  x¯ y p + x y p  

  =   y p

So C = x p + x y + y p

In case of K-Map for 'S' there are no adjacencies. So

       S =  x¯y¯ p +  x¯yp¯  + xy¯p¯ + x y p

Until now we have determined about addition of bit only however what will happen if we are in fact adding two numbers. A number in computer can be 4 byte it implies that 32 bit long or even more. Even for these cases fundamental unit is full adder. Let's see (e.g.) how can we create an adder that adds two 4 bit numbers. Let's presume the numbers are:  x₃ x₂ x₁ x₀ and y₃ y₂ y₁ y₀ here x_i and y_i (i = 0 to 3) express a bit. 4-bit adder is displayed in figure.

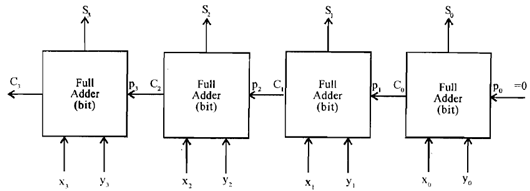
Figure:  4-bit Adder

Overall sum is expressed by S₃ S₂ S₁ S₀ and over all carry is C₃ from 4th bit adder. The main feature of this adder is that carry of every lower bit is fed to subsequent higher bit addition phase it means that addition of next higher bit has to wait for previous stage addition. This is known as ripple carry adder. Ripple carry becomes time consuming when we are going for addition of let's say 32 bit. Here most important bit it implies that 32^nd bit has to wait until addition of first 31 bits is complete. 

Consequently a high-speed adder that produces input carry bit of any stage directly from input to previous stages was created. These are known as carry look ahead adders. In this adder carry for several stages can be produced directly by logic expressions for example:

C0   = x₀ y₀

C1   = x₁ y₁ + (x₁ + y₁) C₀

Complexity of look ahead carry bit raises with higher bits. However in turn it generates the addition in a very small time. Carry look ahead becomes increasingly complex with increasing numbers of bits. So carry look ahead adders are generally implemented for adding chunks of 4 to 8 bits and carry is rippled to subsequent chunk of 4 to 8 bits carry look ahead circuit.