Q. Describe about Boltzmann constant?
The constant η in Figure (b) stands for the noise power spectral density, expressed in terms of power per unit frequency (W/Hz). Statistical theory shows that
η = kT
where k is the Boltzmann constant given by 1.381 × 10-23 J/K and T is the source temperature in kelvins. Equation suggests that a hot resistance is noisier than a cool one, which is compatible with our notion of thermally agitated electrons. At room temperature T0 ≅ 290 K (17° C), η0 works out as 4 × 10-21 W/Hz.
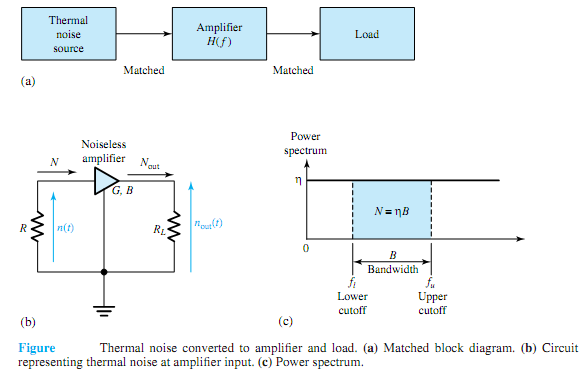
When we employ amplifiers in communication systems to boost the level of a signal, we are also amplifying the noise corrupting the signal. Because any amplifier has some finite passband, we may model an amplifier as a filter with frequency response characteristic H(f). Let us evaluate the effect of the amplifier on an input thermal noise source.
Figure (a), in block diagram form, illustrates a thermal noise source connected to a matched two-port network having frequency response H(f) and the output of the network connected to a matched load. Figure (b) shows a thermal noise source represented by a resistance R connected to an amplifier with a matched input resistance. Presuming the amplifier to be noiseless, with power gain G and bandwidth B, the output noise power is
Nout = GN = GηB
where N = ηB represents the source noise power [the area under the power-spectrum curve falling within the passband, as shown in Figure (c)] accepted by the amplifier as input. The rms noise voltage for a thermal source connected to a matched resistance is then given by
ηrms = √RkTB
The open-circuit voltage would be twice this value.