Chain Rule : We've seen many derivatives.  However, they have all been functions similar to the following kinds of functions.

R ( z ) = √z      f (t ) = t ⁵⁰                    y = tan ( x )         h ( w) = e^w       g ( x ) =ln x

These are all rather simple functions in that wherever the variable appears it is by itself.  What about functions as the below given,

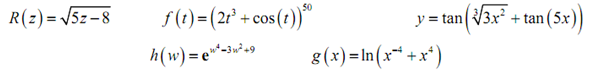
On these functions none of our rules will work and still some functions are closer to the derivatives which we're liable to run into than the functions in the first set.

For example let's take the first one.  On the definition of the derivative actually we used the definition to calculate this derivative. In that section we found that,

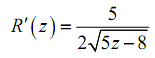
If we were to only utilizes the power rule on this we would get,

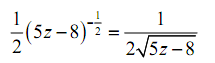
that is not the derivative which we computed using the definition.  It is close, although it's not the similar.  Thus, the power rule alone won't work simply to get the derivative here.

Let's keep looking at this function and note as well that if we define,

f ( z )= √z        g ( z ) = 5z - 8

then we can write function as a composition.

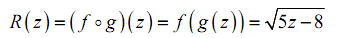
and it turns out that actually it's fairly simple to differentiate a function composition by using the Chain Rule. There are two forms of chain rule.  Following they are.