Derivative for the trig function: We'll begin with finding the derivative of the sine function. To do this we will have to utilize the definition of the derivative. It's been whereas since we've had to utilize this, however sometimes there just isn't anything we can do regarding it.  Following is the definition of the derivative for the sine function.

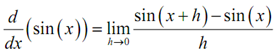
As we can't just plug in h = 0 to evaluate the limit we will have to use the given trig formula on the first as in the numerator.

sin ( x + h ) = sin ( x ) cos ( h ) + cos ( x ) sin ( h )

Doing this gives us,

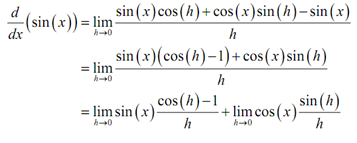
As you can see upon by using the trig formula we can combine the first & third term and then factor out sine of that. Then we can break up the fraction in two pieces, both of which can be dealt separately.

Now, here both of the limits are limits as h approaches zero.  In the first limit we contain a sin(x) and in the second limit we contain a cos(x).  Both of these are just functions of x only and as h moves in towards zero it has no affect on the value of x. Thus, as far as the limits are concerned, these two functions are constants & can be factored out of their respective limits.

Doing this gives,

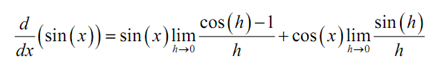
At this point all we have to do is utilizes the limits in the fact above to finish out this problem.

d (sin ( x )) / dx= sin ( x ) (0) + cos ( x ) (1)= cos ( x )

Differentiating cosine is completed in a similar fashion. It will need a different trig formula, however other than that is an almost identical proof. While done with the proof you should get,

                                           d (cos ( x )) / dx= - sin ( x )

Along with these two out of the way the remaining four are rather simple to get.  Remaining four trig functions can be explained in terms of sine & cosine and these definitions, along with suitable derivative rules, can be utilized to get their derivatives.

Let's take a look at tangent. Tangent is explained as,

                                              tan ( x ) = sin ( x ) /cos ( x )

Now that we have the derivatives of sine & cosine all that we have to do is use the quotient rule on this.  Let's accomplish that.

d ( tan (x ))/ dx = d ( sin ( x ) /cos(x))/dx

                           = cos ( x ) cos ( x ) - sin ( x )(- sin ( x )) /cos ( x ))²

                           = cos² ( x ) + sin ² ( x ) /cos² ( x )

Now, recall that cos² ( x ) + sin ² ( x )= 1 and if we also recall the definition of secant in terms of cosine we arrive at,

d ( tan(x))/dx= cos² ( x ) + sin ²( x ) /cos2 ( x )

                       = 1/cos² (x )

                       = sec² ( x )

The remaining three trig functions are also quotients including sine and/or cosine and hence can be differentiated in a same manner.  Following are the derivatives of all six of the trig functions.

Derivatives of the six trig functions

d (sin ( x ))/dx = cos ( x )              d (cos ( x )) /dx = - sin ( x )

d ( tan ( x )) /dx= sec² ( x )                    d (cot ( x )) /dx= -csc ² ( x )

d (sec ( x )) = sec (x) tan ( x )           d (csc ( x )) = -csc (x) cot ( x )